By Damir Šegon, Denis Vida, Paul Roggemans, James M. Scott, Jeff Wood
Abstract: A new meteor shower on a Jupiter Family Comet type orbit (TJ = 2.53) has been detected during 2025 September 9 – October 1, by the Global Meteor Network. 377 meteors belonging to the new shower were observed between 166° < λʘ < 188° from a radiant at R.A. = 43° and Decl.= –66°, with a geocentric velocity of 22.1 km/s. Maximum activity occurred at λʘ = 181.3° (September 24). The new meteor shower has been listed in the IAU MDC Working List of Meteor Showers under the temporary name-designation: M2025-S2.
1 Introduction
The GMN radiant maps for September 20 – 21, 2025, showed a clear concentration of related radiants in the constellation of Hydrus. Initially 109 meteors of this meteor shower were observed by the Global Meteor Network low-light video cameras during the period 2025 September 12 – 21. The shower was independently observed by cameras in five countries (Australia, Brazil, Chile, New Zealand and South Africa).
The shower had a median geocentric radiant with coordinates R.A. = 31.6°, Decl. = –66.9 (equinox J2000.0) at its discovery. The radiant drift in R.A. was +1.64° on the sky per degree of solar longitude and +0.29° in Dec., both referenced to λʘ = 175.3°. The median Sun-centered ecliptic coordinates were λ – λʘ = 156.5°, β = –67.8°. The geocentric velocity was 20.6 ± 0.1 km/s. The new meteor shower was reported to the IAU-MDC and registered under the temporary identification 2025-S2.
The new shower didn’t fade in activity, but grew stronger and lasted for more than a week after being reported to the IAU-MDC. The radiant showed a remarkable strong drift in Sun-center ecliptic coordinates. A new analysis was required to cover the entire activity period.
2 The GMN shower association method
The GMN shower association criteria assumes that meteors within 1° in solar longitude, within 4.8° in radiant in this case, and within 10% in geocentric velocity of a shower reference location are members of that shower. Further details about the shower association are explained in Moorhead et al. (2020). These are a rather strict criteria since meteor showers often have a larger dispersion in radiant position and velocity. Using these meteor shower selection criteria, 377 orbits have been associated with the new shower in the GMN meteor orbit database in a second analysis.
The activity period lasted from September 9 to October 1 starting with the radiant in the constellation Tucana moving through Hydrus and Horologium and ending in Reticulum. When the new shower was first reported its radiant was in Hydrus, but the maximum activity occurred later at λʘ = 181.3° when the radiant was located in Reticulum. The folklore of naming a meteor shower to a star near its radiant will be like a lottery in this case.
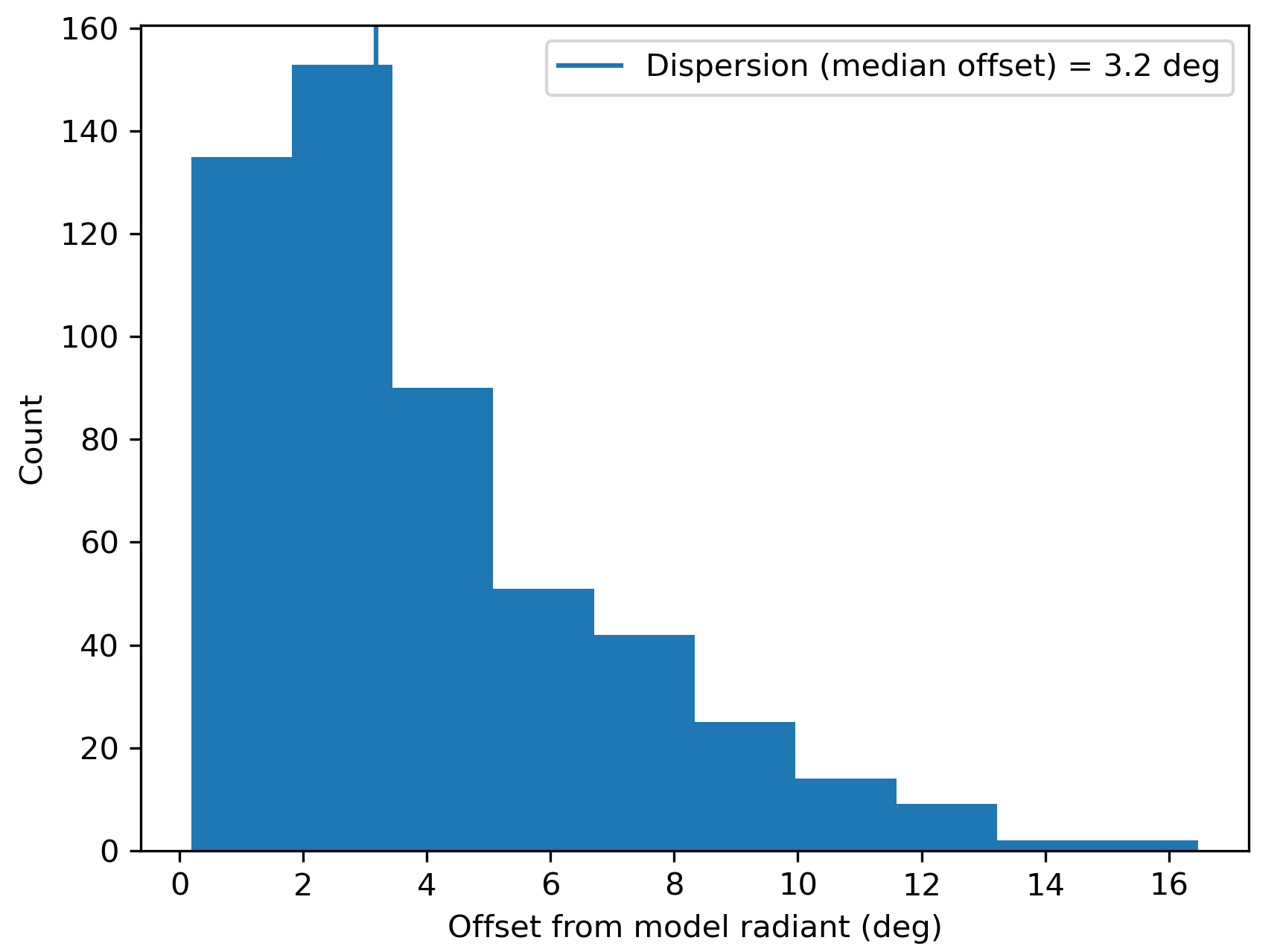
Figure 1 – Dispersion median offset on the radiant position.
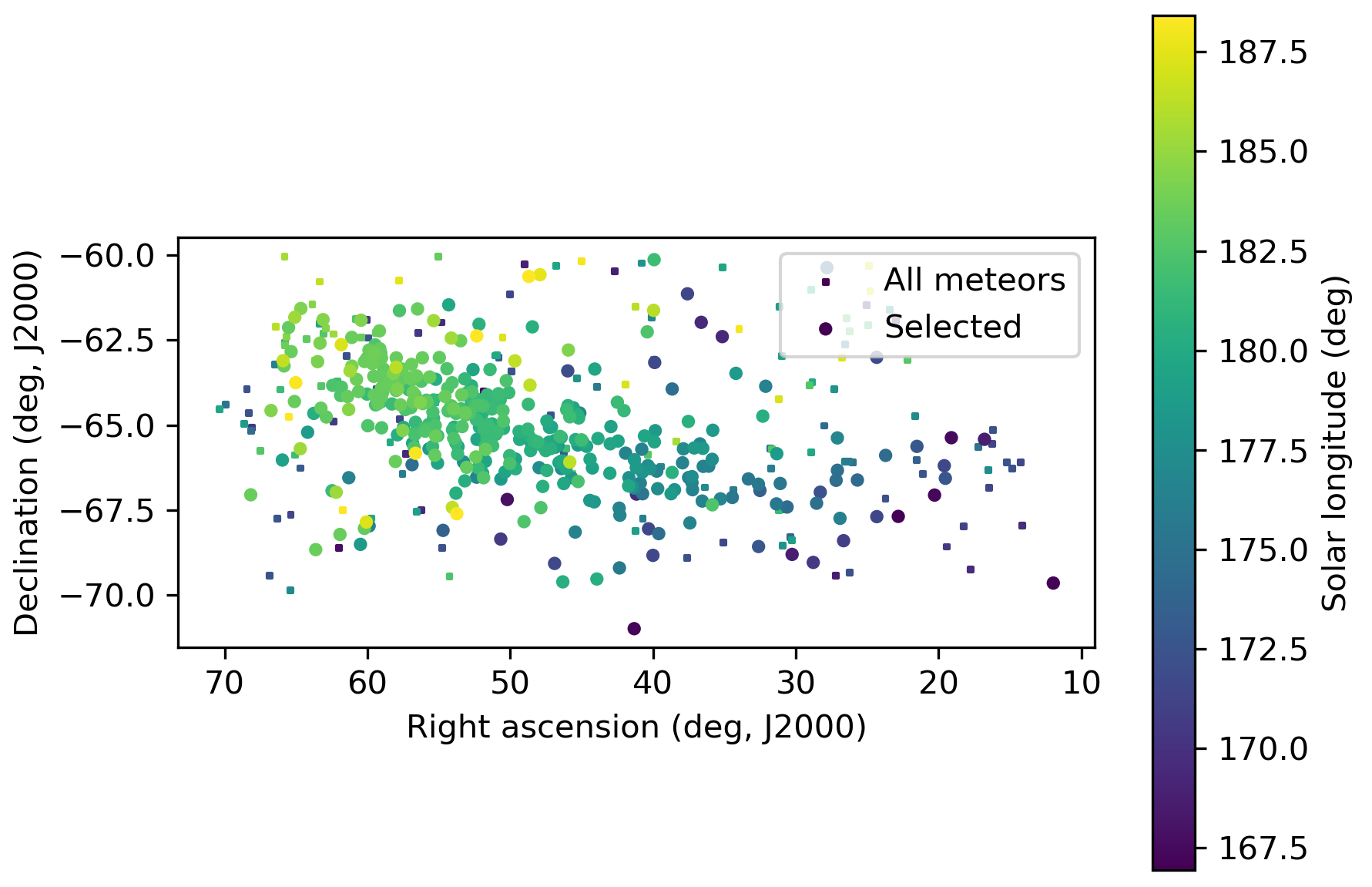
Figure 2 – The radiant distribution during the solar-longitude interval 167° – 188° in equatorial coordinates.

Figure 3 – The radiant drift.
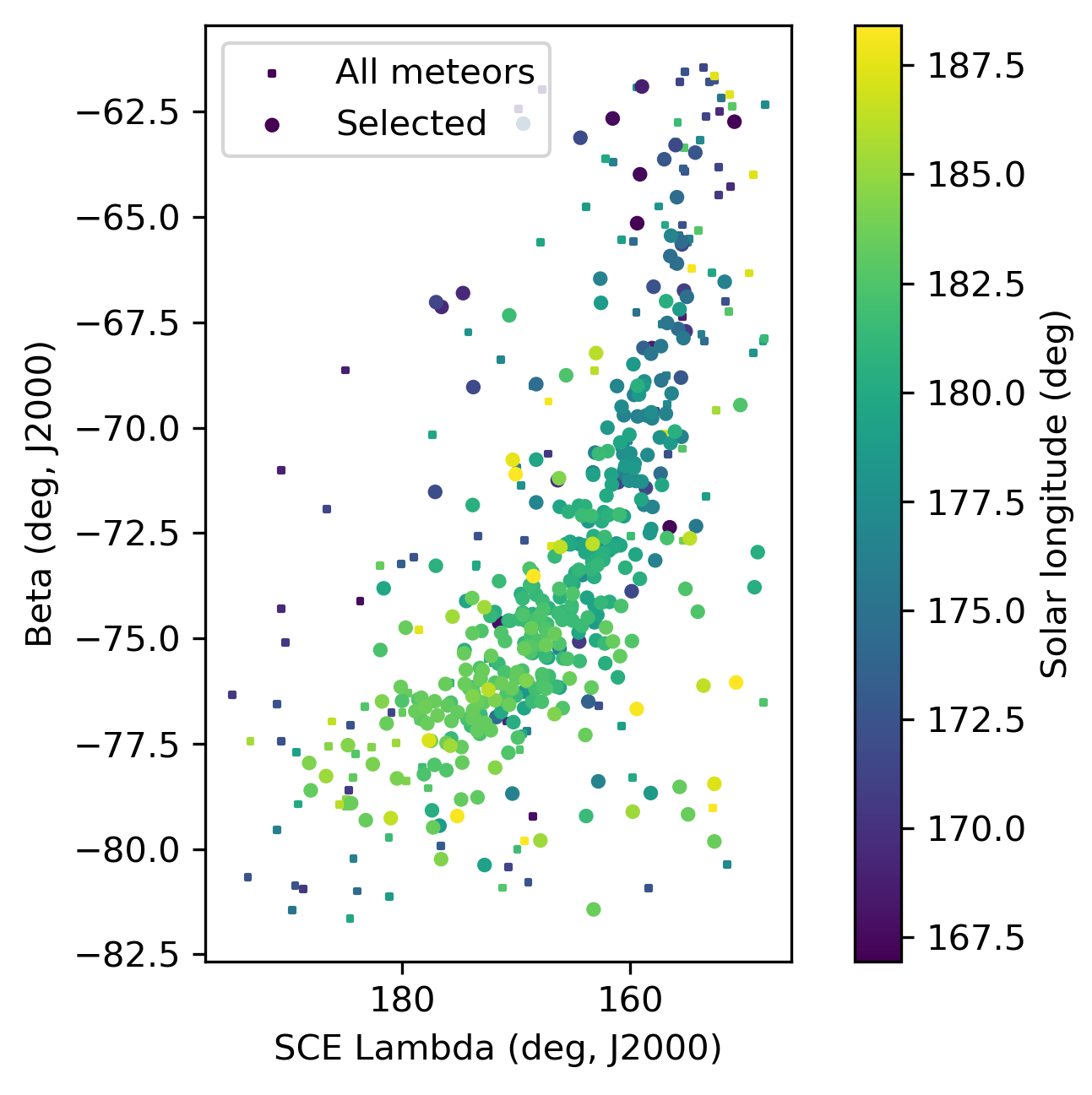
Figure 4 – The radiant distribution during the solar-longitude interval 167° – 188° in Sun centered geocentric ecliptic coordinates.
The new GMN analysis resulted in a median geocentric radiant with coordinates R.A. = 42.9°, Decl. = –65.9 (equinox J2000.0) (Figure 2). The radiant drift in R.A. was +1.96° on the sky per degree of solar longitude and +0.22° in Dec., both referenced to λʘ = 177.0° (Figure 3). The median Sun-centered ecliptic coordinates were λ – λʘ = 163.6°, β = –71.5°. The geocentric velocity was 22.1 ± 0.1 km/s. The Sun-centered ecliptic coordinates show a remarkably strong radiant drift with Δ(λ – λʘ) = 0.84°, Δβ = –0.65° forming a long extended radiant in the shape of a sickle (Figure 4).
3 Another search method
Meteor shower identification strongly depends on the methodology used to select candidate shower members. The sporadic background is everywhere present at the sky which risks to contaminate selections of shower candidates. Using a radiant location is a straightforward method to classify shower meteors. In order to double check GMN meteor shower detections, another method, based on orbit similarity criteria is used. This approach serves to make sure that no spurious radiant concentrations are mistaken as new meteor showers.
A reference orbit is required to start an iterative procedure to approach a mean orbit, which is the most representative orbit for the meteor shower as a whole, removing outliers and sporadic orbits. This method has been described before (Roggemans et al., 2019). Three different discrimination criteria are combined in order to have only those orbits which fit the different criteria thresholds. The D-criteria that we use are these of Southworth and Hawkins (1963), Drummond (1981) and Jopek (1993) combined. The values are considered in different classes with different thresholds of similarity:
- Medium Low: DSH < 0.125 & DD < 0.05 & DJ < 0.125;
- Medium high: DSH < 0.1 & DD < 0.04 & DJ < 0.1;
- High: DSH < 0.075 & DD < 0.03 & DJ < 0.075.
- Very high: DSH < 0.05 & DD < 0.02 & DJ < 0.05.
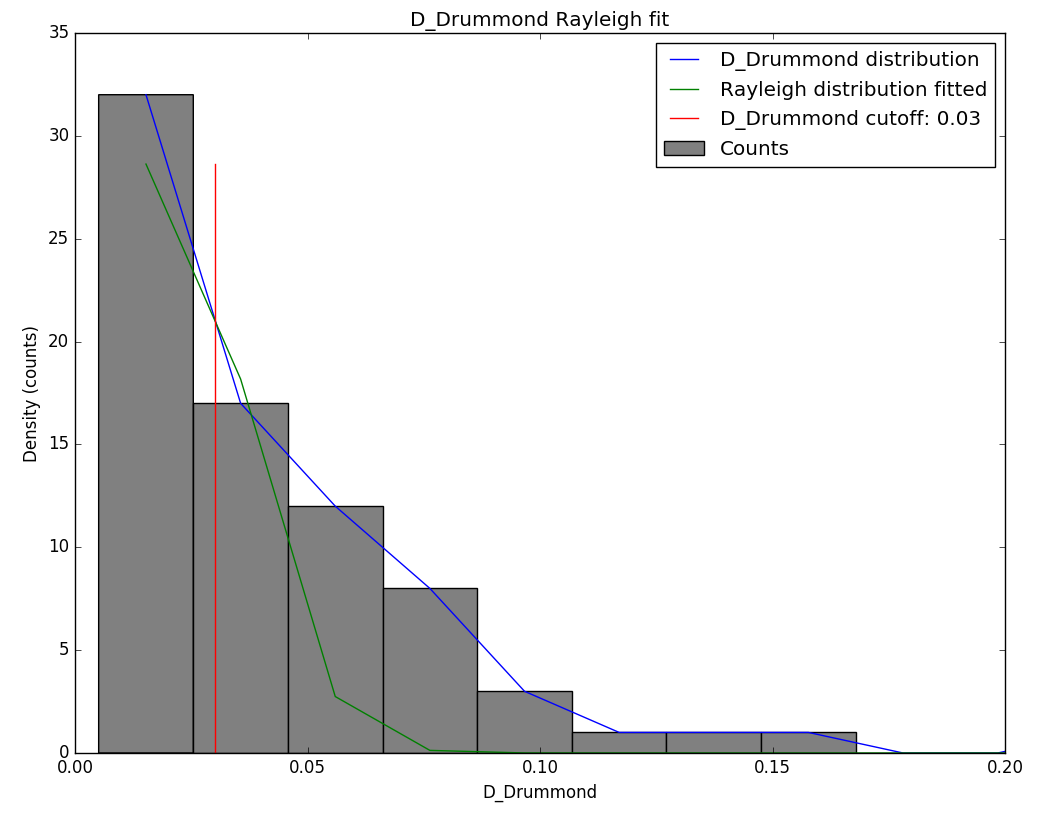
Figure 5 – Rayleigh distribution fit and Drummond DD criterion cutoff.
The Rayleigh distribution fit pointed at a DD value of 0.03 as the orbital similarity threshold value cutoff (Figure 5). The radiant drift in Sun-centered ecliptic coordinates due to changes in orbital elements during Earth’s transit, makes it impossible to describe this meteoroid stream with a single reference orbit. The D-criteria values are no more than an indication for the degree of similarity between an orbit and a reference orbit. Working with D-criteria requires caution like in this case when the orbital elements change significantly during Earth’s transit. Figure 6 shows the changes in the radiant position and appearance during the activity period and requires an adapted approach.
All GMN orbit data was extracted for the time interval of 165° < λʘ < 187°, limited in Sun-centered geocentric ecliptic coordinates with 139° < λ–λʘ < 206° and –57° < β < –84°. The method was applied on four intervals of 7° in solar longitude, with an overlap of 2°:
- 165° < λʘ< 172°
- 170° < λʘ< 177°
- 175° < λʘ< 182°
- 180° < λʘ< 187°
For each time bin a mean orbit was computed as a reference orbit to start the iteration to approach the best fitting mean orbit for each interval. We didn’t use median values to derive a mean orbit since a vectoral solution like the method of Jopek et al. (2006) is more appropriate for orbital elements with angular values. This method resulted in 277 orbits that fit with the mean orbit for each interval within the similarity threshold with DSH < 0.075, DD < 0.03 and DJ < 0.075.
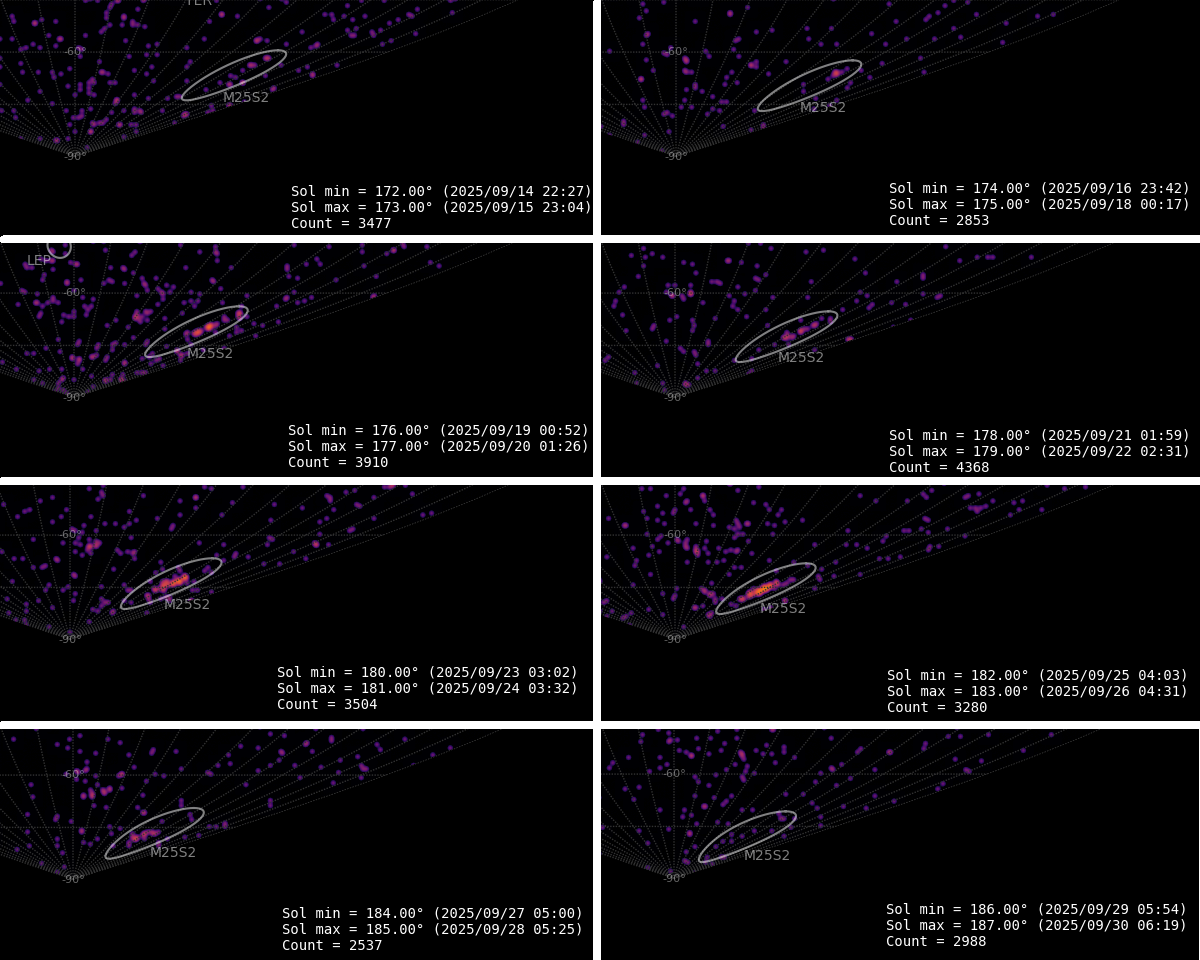
Figure 6 – The evolution of the radiant of M2025-S2 on the GMN radiant density maps during the activity period, plotted in Sun-centered geocentric ecliptic coordinates.
A single solution for the entire activity period is impossible to define with D-criteria since the orbits changed too much during the three weeks of activity. The solutions obtained for each of the four intervals solved the problem. Counting the number of M2025-S2 meteors per solar longitude relative to the total number of meteors recorded at the Southern Hemisphere allows reconstruction of the activity profile. The profiles obtained for the two methods of shower association are superimposed in Figure 7. When the shower was first noticed (at λʘ = 175.0°), the best of the activity had still to come. The skew activity profile indicates maximum activity at λʘ = 181.5° with an abrupt end of the activity after λʘ = 188°. The GMN method associated more meteors as M2025-S2 than the D-criteria method.
Figures 8 to 11 show close-ups and appearance and drift of the radiants for the solution within each interval in solar longitude. The drift of the radiant in Sun-centered longitude and latitude from week to week is clearly visible. The increasing number of radiant dots is in line with the activity profile in Figure 7. Combining all data in a single plot results in a long extended radiant with the shape of a sickle (Figure 12). Note that most radiants correspond to orbits with a very small similarity threshold of DSH < 0.05, DD < 0.02 and DJ < 0.05.
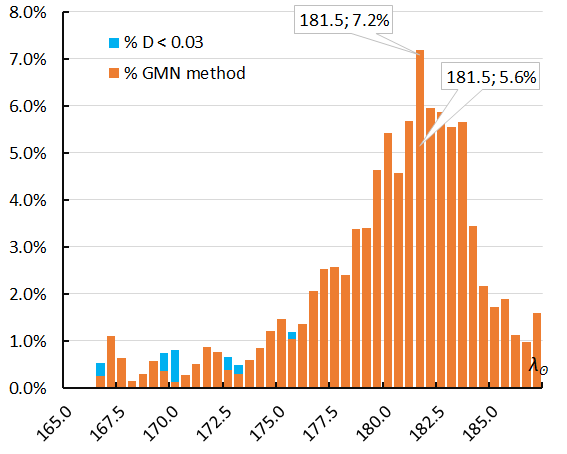
Figure 7 – The percentage of M2025-S2 meteors relative to the total number of meteors recorded by cameras at the Southern Hemisphere. Orange is the result for the GMN shower classification, blue for the D-criteria threshold method.
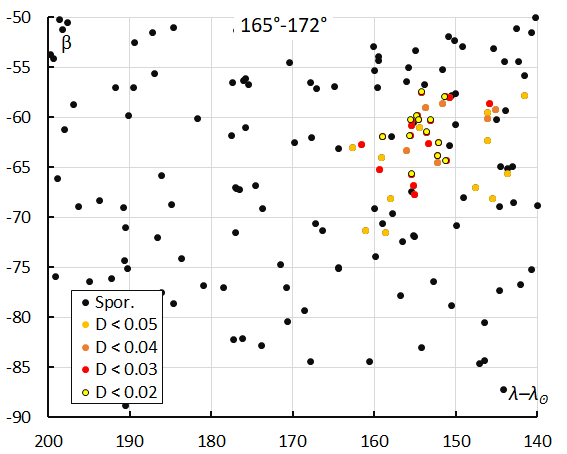
Figure 8 – The radiant distribution during the solar-longitude interval 165° – 172° in Sun centered ecliptic coordinates.
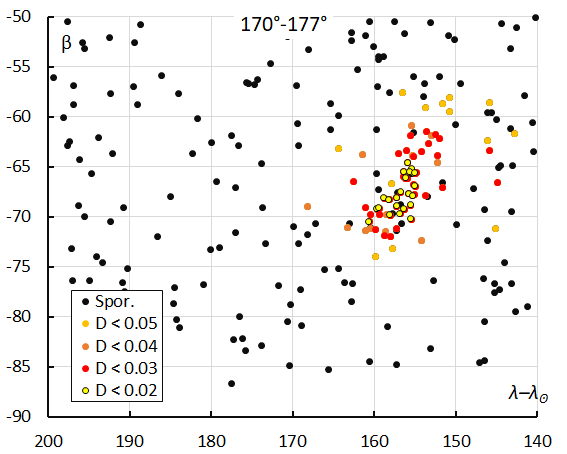
Figure 9 – The radiant distribution during the solar-longitude interval 170° – 177° in Sun centered ecliptic coordinates.
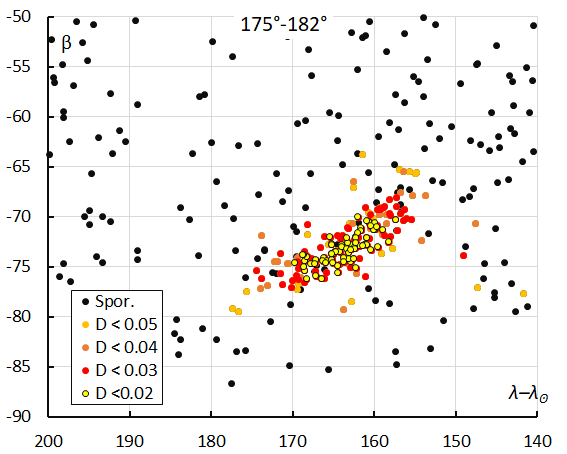
Figure 10 – The radiant distribution during the solar-longitude interval 175° – 182° in Sun centered ecliptic coordinates.
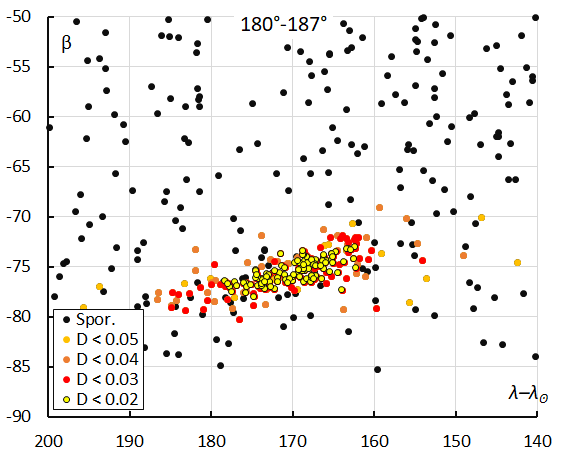
Figure 11 – The radiant distribution during the solar-longitude interval 180° – 187° in Sun centered ecliptic coordinates.
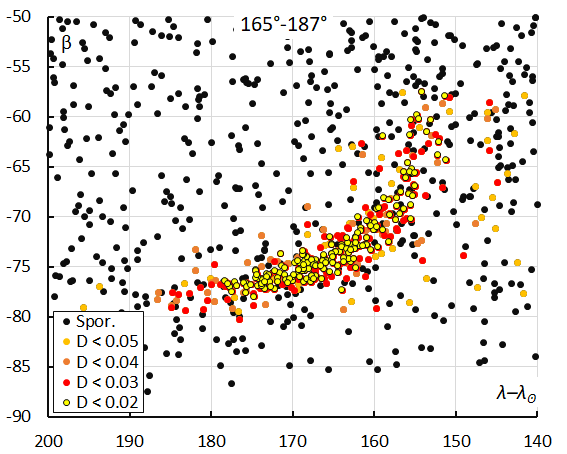
Figure 12 – The radiant distribution during the solar-longitude interval 165° – 187° in Sun centered ecliptic coordinates.
Table 1 – GMN 1st is the solution reported when M2025-S2 was first discovered, GMN 2nd the solution when the activity had ended. The solutions for four intervals in solar longitude were derived from the method described in Section 3, valid for DD < 0.03.
| GMN 1st | GMN 2nd | 165°–172° | 170°–177° | 175°–182° | 180°–187° | |
| λʘ (°) | 175.3 | 181.3 | 170.2 | 175.4 | 180.1 | 182.3 |
| λʘb (°) | 166.9 | 166.9 | 166.7 | 170.5 | 175.4 | 180.0 |
| λʘe (°) | 178.1 | 188.4 | 171.7 | 176.8 | 182.0 | 186.5 |
| αg (°) | 31.6 | 42.9 | 15.2 | 28.5 | 47.3 | 55.2 |
| δg (°) | –66.9 | –65.9 | –66.1 | –66.7 | –65.6 | –64.4 |
| Δαg (°) | 1.64 | 1.96 | 0.75 | 2.64 | 2.78 | 2.99 |
| Δδg (°) | +0.29 | +0.22 | –0.17 | +0.12 | +0.36 | +0.46 |
| vg (km/s) | 20.6 | 22.1 | 19.3 | 20.7 | 22.3 | 23.4 |
| Hb (km) | 93.9 | 95.8 | 93.8 | 94.3 | 95.8 | 96.4 |
| He (km) | 83.1 | 84.1 | 83.1 | 81.8 | 83.5 | 84.1 |
| Hp (km) | 87.0 | 88.3 | 87.4 | 86.4 | 88.3 | 88.5 |
| MagAp | +0.9 | +0.4 | +0.7 | +0.5 | +0.2 | +0.1 |
| λg (°) | 331.83 | 344.89 | 325.1 | 330.9 | 343.6 | 349.9 |
| λg – λʘ (°) | 156.53 | 163.59 | 154.7 | 155.9 | 163.3 | 168.9 |
| βg (°) | –67.82 | –71.48 | –61.9 | –66.9 | –65.6 | –75.5 |
| a (A.U.) | 3.203 | 3.237 | 3.33 | 3.34 | 3.27 | 3.28 |
| q (A.U.) | 0.956 | 0.965 | 0.944 | 0.955 | 0.966 | 0.970 |
| e | 0.701 | 0.702 | 0.717 | 0.714 | 0.705 | 0.704 |
| i (°) | 29.7 | 34.8 | 27.1 | 29.9 | 34.0 | 36.3 |
| ω (°) | 27.6 | 23.7 | 31.1 | 27.9 | 24.2 | 22.5 |
| Ω (°) | 354.1 | 0.4 | 350.1 | 354.7 | 359.8 | 2.4 |
| Π (°) | 21.7 | 24.1 | 21.2 | 22.6 | 24.0 | 24.8 |
| Tj | 2.60 | 2.53 | 2.56 | 2.53 | 2.52 | 250 |
| N | 109 | 377 | 22 | 51 | 131 | 158 |
4 Orbit and parent body
The final mean orbits based on the meteors identified as M2025-S2 according to the GMN method and the D-criteria method for the different intervals in solar longitude are in general in good agreement but show that meteor shower orbit parameters strongly depend on the sample that is used.
Looking at the diagram of inclination versus longitude of perihelion for each interval, we can see the inclination and the longitude of perihelion slightly increasing. The dense concentration just below the M2025-S2 meteors are the chi Cygnids (CCY#757), a shower active at the same time with very similar characteristics but visible at the Northern Hemisphere.
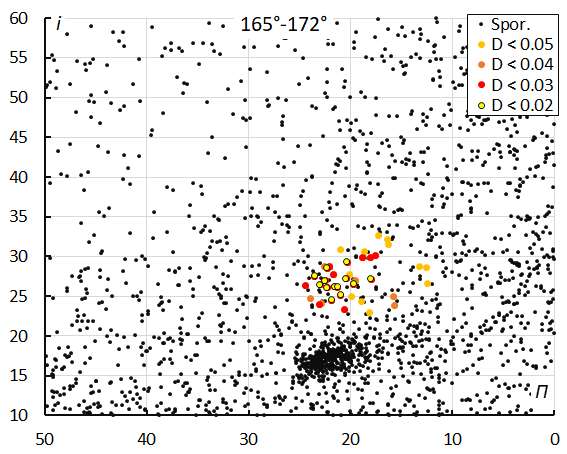
Figure 13 – The diagram of the inclination i against the longitude of perihelion Π color coded for different classes of D criterion threshold, for λʘ between 165° and 172°.
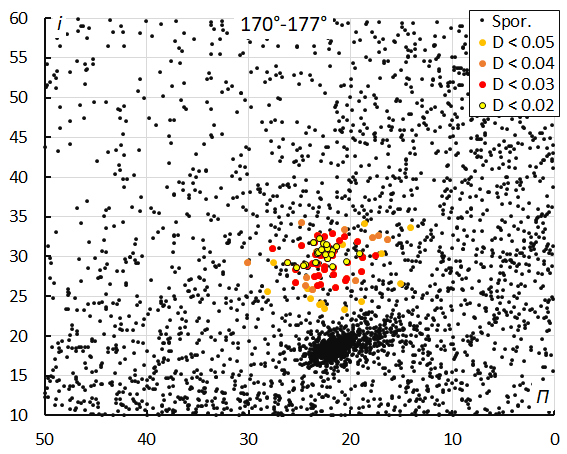
Figure 14 – The diagram of the inclination i against the longitude of perihelion Π color coded for different classes of D criterion threshold, for λʘ between 170° and 177°.
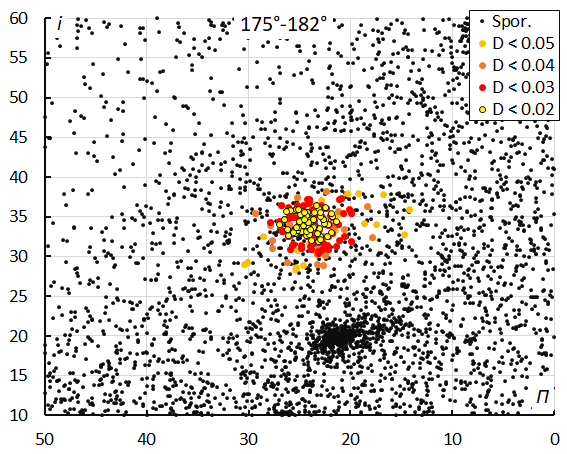
Figure 15 – The diagram of the inclination i against the longitude of perihelion Π color coded for different classes of D criterion threshold, for λʘ between 175° and 182°.
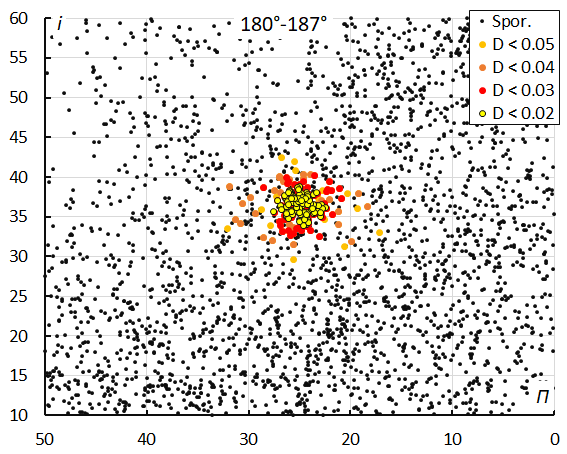
Figure 16 – The diagram of the inclination i against the longitude of perihelion Π color coded for different classes of D criterion threshold, for λʘ between 180° and 187°.
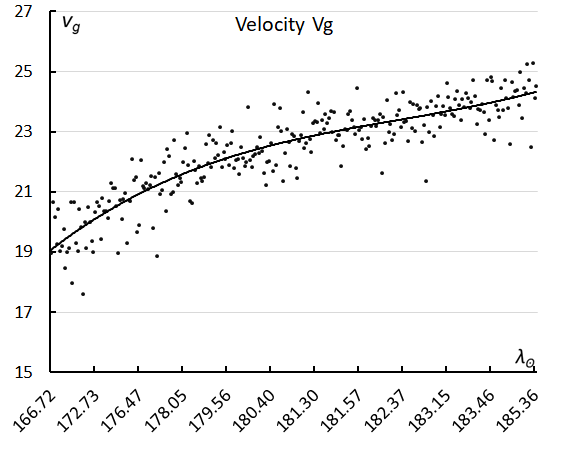
Figure 17 – The geocentric velocity in function of the solar longitude.
During the activity of the M2025-S2 meteor shower, the geocentric velocity increased, from about 19 km/s to more than 24 km/s (Figure 17). The change in velocity is also visible in the plot of the radiants in Sun-centered ecliptic coordinates, which compensate the radiant drift caused by the rotation of the Earth around the Sun. The remarkable strong drift in Sun-centered ecliptic coordinates increased during the activity period from Δ(λ – λʘ) = +0.52°, Δβ = –0.86° in the second week to Δ(λ – λʘ) = 2.85°, Δβ = –0.97° in the last week. The first week had too few data to determine radiant drift. This change in drift explains the sickle shaped radiant plot in Figure 18.
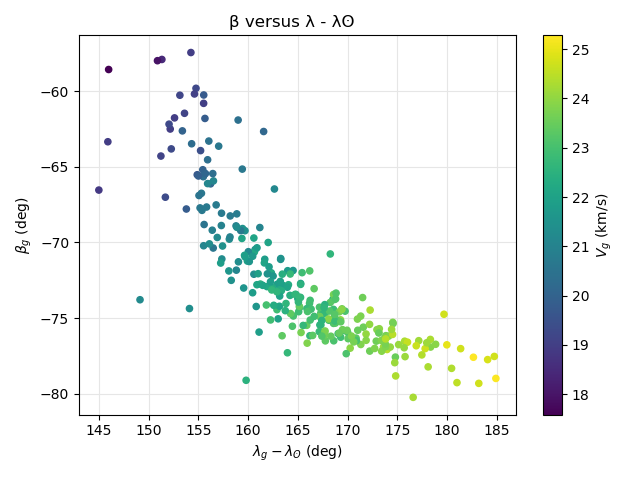
Figure 18 – The radiant distribution during the solar-longitude interval 165° – 187° in Sun centered ecliptic coordinates, color-coded in function of the geocentric velocity.
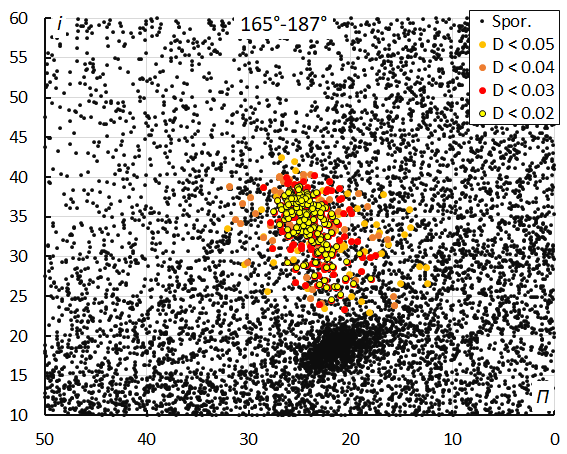
Figure 19 – The diagram of the inclination i against the longitude of perihelion Π color-coded for different classes of D criterion threshold, for λʘ between 165° and 187°.
Figure 19 seem to shows how the orbits changed in inclination and longitude of perihelion during the entire activity period. In reality, the orbits are rather concentrated if considered in short time intervals. The dispersion is due to the rapid change in inclination and longitude of perihelion. This drift in inclination is shown in Figure 20 and in longitude of perihelion in Figure 21. Both line graphs show the evolution in time.
Figure 22 shows the same diagram as Figure 19 but color-coded for velocity. At the start of the activity slower M2025-S2 meteors have a lower inclination and smaller longitude of perihelion. Towards the end of the shower activity these meteors are much faster with a higher inclination and larger longitude of perihelion.
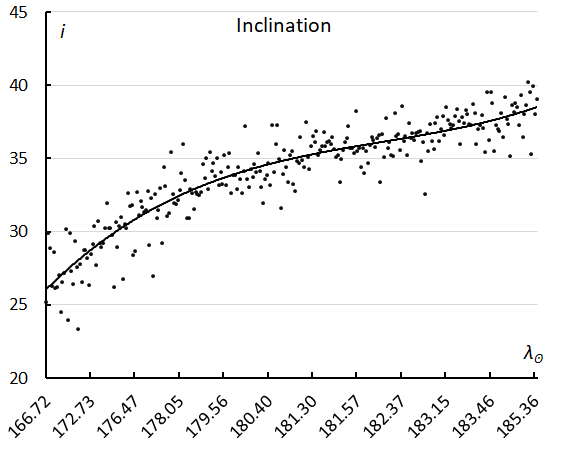
Figure 20 – The inclination i in function of the solar longitude.
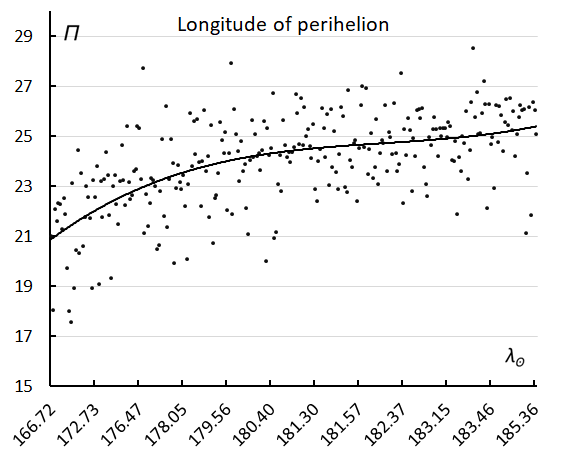
Figure 21 – The longitude of perihelion Π in function of the solar longitude.
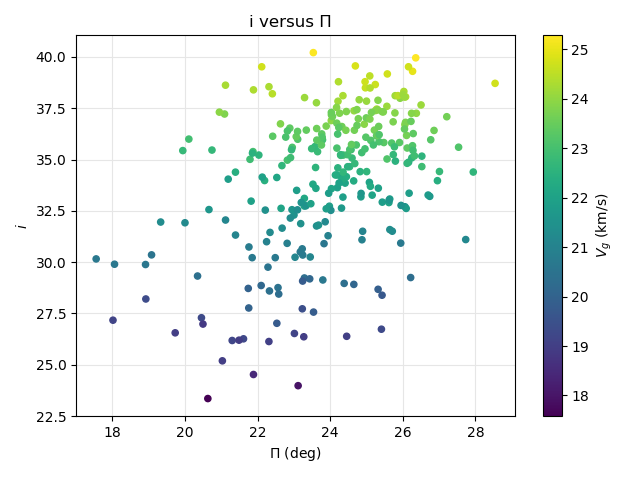
Figure 22 – The diagram of the inclination i against the longitude of perihelion Π, color-coded in function of the geocentric velocity.
Figure 23 shows less dispersion in eccentricity than in inclination (Figure 19). The eccentricity seems to decrease slightly during the activity period (Figure 24). There is some correlation between the velocity and the longitude of perihelion, but in eccentricity the velocity looks randomly distributed. The dense concentration immediately right-below of the M2025-S2 concentration are again the chi Cygnids (CCY#757).
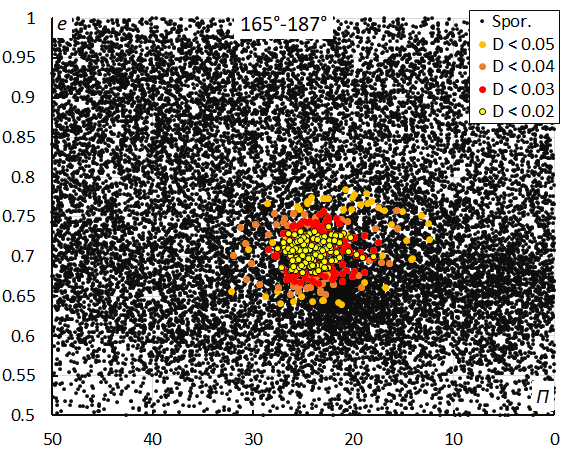
Figure 23 – The diagram of the eccentricity e against the longitude of perihelion Π color-coded for different classes of D criterion threshold, for λʘ between 165° and 187°.
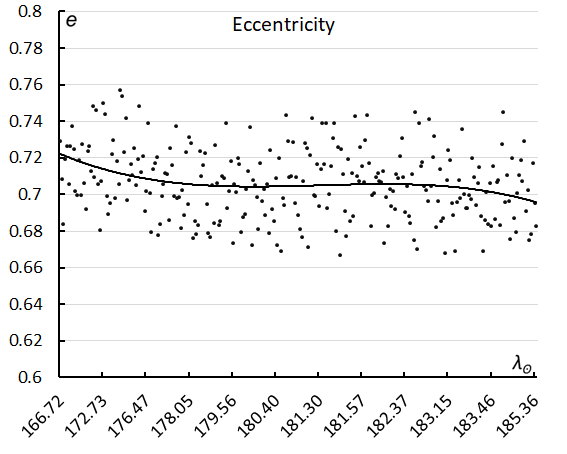
Figure 24 – The eccentricity e in function of the solar longitude.
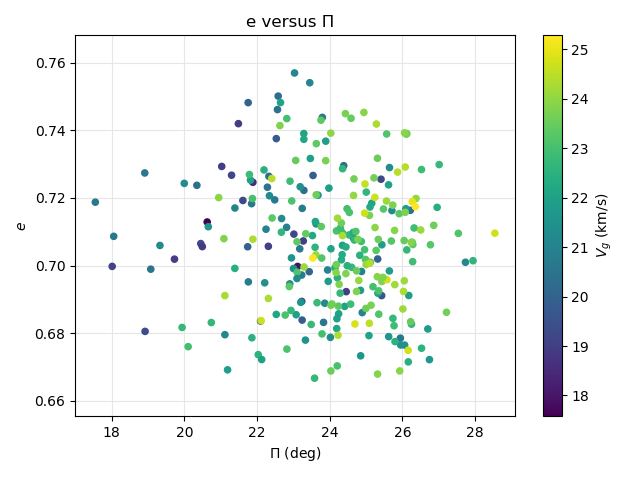
Figure 25 – The diagram of the eccentricity e against the longitude of perihelion Π, color-coded in function of the geocentric velocity.
Looking at the diagram of the eccentricity versus the inclination the orbits appear mainly dispersed in inclination (Figure 26). The dense concentration of orbits just left from the M2025-S2 orbits, are the chi Cygnids (CCY#757) which have a slightly lower inclination and eccentricity. The drift in velocity is mainly visible in the inclination in Figure 27. The faster the meteors the higher the inclination.
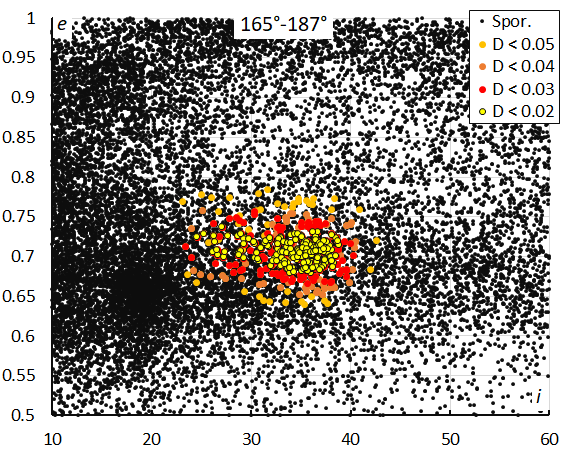
Figure 26 – The diagram of the eccentricity e against the inclination i color-coded for different classes of D criterion threshold, for λʘ between 165° and 187°.
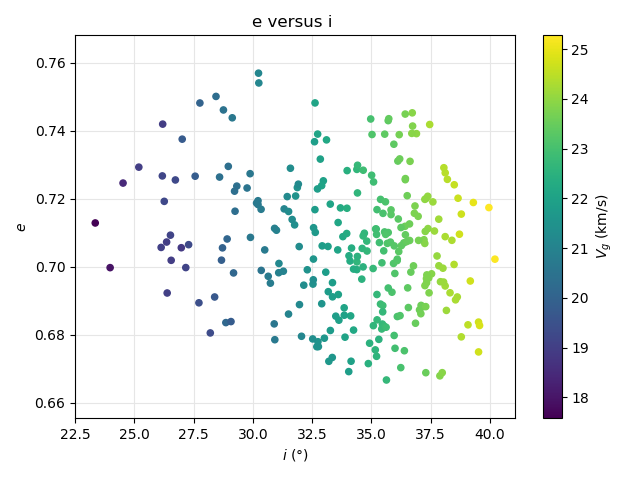
Figure 27 – The diagram of the eccentricity e against the inclination i, color-coded in function of the geocentric velocity.
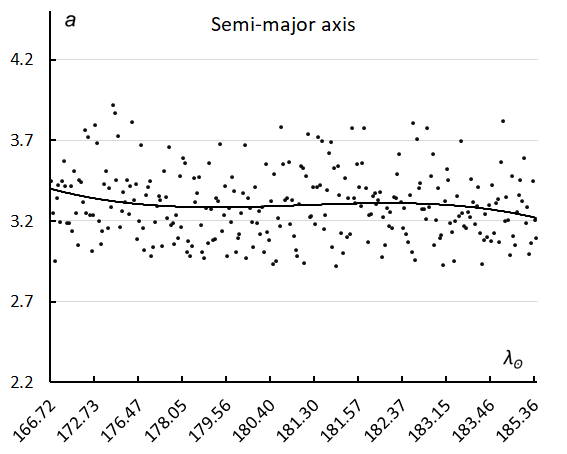
Figure 28 – The semi-major axis a in function of the solar longitude.
During the shower activity we see no significant change in semi-major axis a (Figure 28). There is a clear increase in perihelion distance q. The diagram of the perihelion distance versus the inclination shows a long-stretched trail in both inclination and perihelion distance. The dark concentration left from M2025-S2 are again the chi Cygnids (Figure 29).
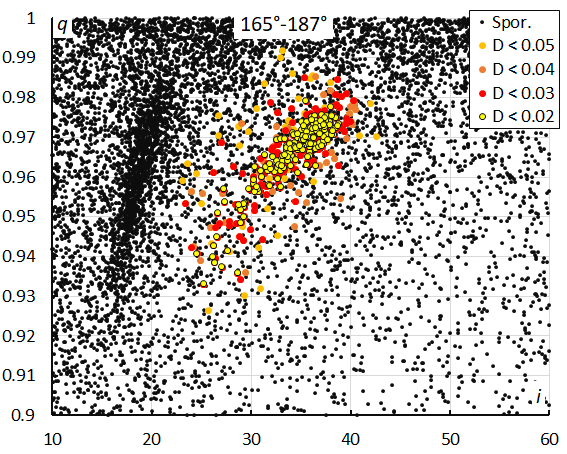
Figure 29 – The diagram of the perihelion distance q against the inclination i color-coded for different classes of D criterion threshold, for λʘ between 165° and 187°.
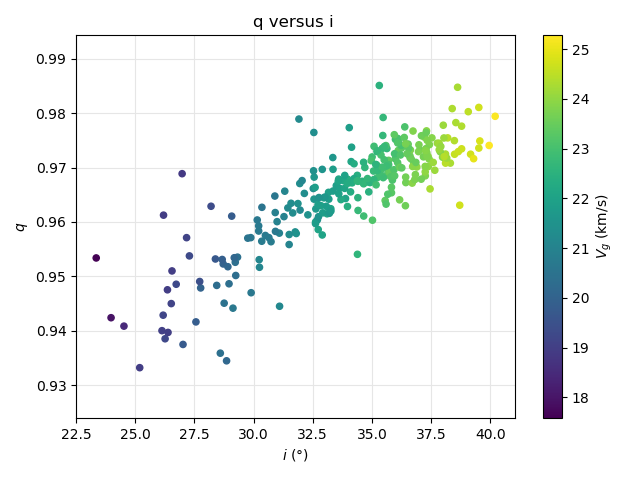
Figure 30 – The diagram of the perihelion distance q against the inclination i, color-coded in function of the geocentric velocity.
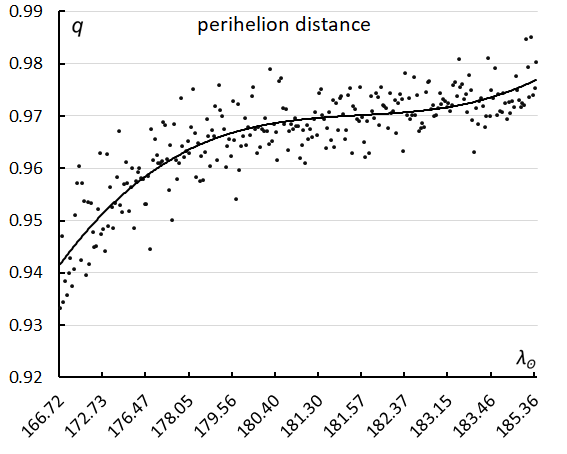
Figure 31 – The perihelion distance q in function of the solar longitude.
Figures 30 and 31 combined show how the perihelion distance and inclination increase with the velocity during the activity period of M2025-S2.
Figures 8 to 31 were all derived from the selection based on the method with D-criteria, which has 277 M2025-S2 meteors against the GMN method which has 377. Only 6 meteors selected by D-criteria were ignored by the GMN method. 106 meteors identified by the GMN method were not detected by the D-criteria method, of which ten orbits do not even fit the low threshold class similarity for the mean orbit obtained by the GMN method. The rapidly changing orbit parameters during the activity makes it impossible to apply D criteria on a single solution reference orbit. Therefore, the activity period has been split into four intervals in solar longitude. The solutions for the two methods correspond best for the interval 175°-182°.
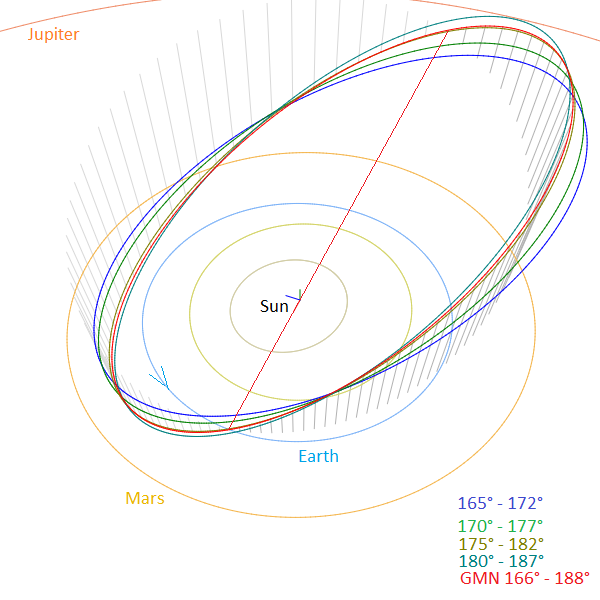
Figure 32 – Comparing the mean orbits for the solutions for M2025-S2 based on the shower identification according to two methods, red for the 2025GMN solution, the other colors for the intervals used for the D-criteria shower search method with DD < 0.03 in Table 1, close-up at the inner Solar System. (Plotted with the Orbit visualization app provided by Pető Zsolt).
The Tisserand’s parameter relative to Jupiter, Tj (= 2.53) identifies the orbit as of a Jupiter Family Comet type orbit. Figure 32 shows the orbits for the different solutions in the inner solar system. The dust of M2025-S2 crosses the Earth orbit at its ascending node from south of the ecliptic radiating from a circumpolar radiant at the Southern Hemisphere. Comparing the orbits for the different time bins in solar longitude, we see that the orbital plane gradually changes in orientation. This layered structure is what we see in the changing orbital parameters and the strong drift in Sun-centered ecliptic coordinates during the activity period. The mean orbit obtained by the GMN method is very close to the solution for the time interval 175°–182° obtained with the D-criteria method.
The orbit crosses the ecliptic at its descending node close to the orbit of Jupiter, which means that dust trails will be much affected by this giant planet’s gravitational perturbations. Although the Jupiter Family Comet type orbit suggests a cometary origin, meteoroids of M2025-S2 have a deep ablation height in the atmosphere uncommon for fragile cometary material.
Three other sources observed around the same time, the epsilon Ursae-Minorids (EPU#1044) (Roggemans et al., 2025a), M2024-S1 discovered in 2024 (Vida and Šegon, 2024; Šegon et al., 2025) and observed again in 2025 (Roggemans et al., 2025b) and the chi Cygnids (CCY#757) were all three in outburst in 2025. All three cross the Earth orbit at their descending node at about the same time as M2025-S2 crossed its ascending node. All these meteoroid streams cross the ecliptic near the Earth orbit at one node and have the position of the other node as well as the aphelion relatively close to the orbit of Jupiter. All have the same characteristic with meteors penetrating deep into the atmosphere. The epsilon Ursae-Minorids and chi Cygnids are known as episodic showers. It would be worthwhile to run orbit integrations to understand the mechanism that gave these showers their periodic nature and peculiar characteristics.
A list of possible parent bodies is listed in Table 2. Stream modelers may reconstruct the dynamics of this meteoroid stream. It is uncertain if the parent body still exists or if it has already been discovered. There is no convincing evidence among the known candidates in Table 2.
Table 2 – Top ten matches of a search for possible parent bodies with DD < 0.13.
| Name | DD |
| 2022 SJ48 | 0.099 |
| 1994 RB | 0.105 |
| 2017 TO4 | 0.113 |
| 2020 WB3 | 0.116 |
| 2010 UY6 | 0.117 |
| 2009 RD4 | 0.121 |
| 2014 SO260 | 0.122 |
| 2011 TA4 | 0.123 |
| 2019 WF1 | 0.125 |
| 2014 SM142 | 0.127 |
5 Past observations
The Global Meteor Network got good coverage at the Southern Hemisphere since 2022, but only a few orbits could be associated with M2025-S2 in past years (three in 2024 and two in 2023). No other video camera network data is available for the Southern Hemisphere for earlier years. There are visual observations from the 20th century mentioning activity from this part of the sky. The first possible sightings may have been from Cuno Hoffmeister in Namibia in 1938 with a radiant at RA 48° and decl.–68° at λʘ 167.9° (eq.1925). No later possible sightings could be found from South Africa or New Zealand. Michael Buhagiar in the 1970’s made mention that there may be a weak shower in later September near the South Celestial Pole but didn’t provide any details just an opinion/feeling. Others, like WAMS/NAPOMS observers in Australia either didn’t report activity from this part of the sky, or the radiant positions don’t fit with our data. We can conclude that there are no records that reveal any striking activity from M2025-S2 in the past. Its sudden appearance in 2025 may indicate this is a dust trail with a periodic nature or a one-year event.
6 Conclusion
Activity from a new meteor shower M2025-S2 discovered by Global Meteor Network has been analyzed by two different meteor shower association methods. The shower displayed an exceptional strong radiant drift in Sun-centered ecliptic coordinates. During the three weeks activity period the shower gradually increased in activity to reach its maximum activity at λʘ = 181.3° (2025, September 24). The orientation of the orbital plane of the meteoroid stream changes during Earth’s transit and resulted in rapidly changing inclination, longitude of perihelion and distance of perihelion. This layered structure is very similar to the chi Cygnids active at the Northern Hemisphere around the same time.
Acknowledgment
This report is based on the data of the Global Meteor Network (Vida et al., 2020a; 2020b; 2021) which is released under the CC BY 4.0 license. We thank all 825 participants in the Global Meteor Network project for their contribution and perseverance. A list with the names of the volunteers who contribute to GMN has been published in the 2024 annual report (Roggemans et al., 2025).
References
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Jopek T. J., Rudawska R. and Pretka-Ziomek H. (2006). “Calculation of the mean orbit of a meteoroid stream”. Monthly Notices of the Royal Astronomical Society, 371, 1367–1372.
Moorhead A. V., Clements T. D., Vida D. (2020). “Realistic gravitational focusing of meteoroid streams”. Monthly Notices of the Royal Astronomical Society, 494, 2982–2994.
Roggemans P., Johannink C. and Campbell-Burns P. (2019a). “October Ursae Majorids (OCU#333)”. eMetN Meteor Journal, 4, 55–64.
Roggemans P., Campbell-Burns P., Kalina M., McIntyre M., Scott J. M., Šegon D., Vida D. (2025a). “Global Meteor Network report 2024”. eMetN Meteor Journal, 10, 67–101.
Roggemans P., Vida D., Šegon D. (2025b). “Epsilon-Ursae Minorids (EPU#1044) enhanced activity in 2025”. eMetN Meteor Journal, 10, to be published.
Roggemans P., Vida D., Šegon D. (2025c). “M2024-S1 activity confirmed in 2025”. eMetN Meteor Journal, 10, to be published.
Šegon D., Vida D., Roggemans P. (2025). “New meteor shower in Ursa Minor 23–24 September 2024”. eMetN Meteor Journal, 10, 12–19.
Southworth R. B. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithsonian Contributions to Astrophysics, 7, 261–285.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020a). “Estimating trajectories of meteors: an observational Monte Carlo approach – I. Theory”. Monthly Notices of the Royal Astronomical Society, 491, 2688–2705.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020b). “Estimating trajectories of meteors: an observational Monte Carlo approach – II. Results”. Monthly Notices of the Royal Astronomical Society, 491, 3996–4011.
Vida D., Šegon D., Gural P. S., Brown P. G., McIntyre M. J. M., Dijkema T. J., Pavletić L., Kukić P., Mazur M. J., Eschman P., Roggemans P., Merlak A., Zubrović D. (2021). “The Global Meteor Network – Methodology and first results”. Monthly Notices of the Royal Astronomical Society, 506, 5046–5074.
Vida D., Šegon D. (2024). New meteor shower M2024-S1 in Ursa minor. CBET 5452. D. W. E. Green (ed.), 1 pp.