Abstract: The CAMS BeNeLux network captured 6773 meteors in the night of 2018 October 8-9 during the Draconid outburst. A total of 1391 meteor orbits could be obtained. A procedure was applied to locate groups of very similar Draconid orbits. Five compact groups of almost identical and three groups with slightly more dispersed Draconid orbits could be distinguished. Using a range of the mean orbits of these groups as reference orbits, 938 orbits were associated with Draconids. The activity profile shows some sub-maxima, the radiant structure, the velocity distribution and the orbital elements indicate the presence of different dust trails.
1 Introduction
Weather brought clear sky over the BeNeLux for the night of October 8–9, 2018, ideal to observe a possible outburst predicted by Egal et al. (2018). The predicted outburst took place and the spectacle exceeded the expectations. The CAMS BeNeLux network was ideally situated to cover the event. With 80 of its cameras installed at 20 sites, 6773 meteors were detected, 4071 (60%) of these proved to be good quality multi-station events resulting in 1391 orbits which respected the CAMS quality standards (Jenniskens et al., 2011). Immediately after the event observing reports got published (Johannink, 2018; Martin, 2019; Miskotte, 2019a; Roggemans, 2018; Vida et al., 2018). A detailed analysis of the Draconid activity in 2018, based on visual observations resulted in an activity profile with ZHR values well above 100 with some sub-maxima (Miskotte, 2019b).
2 Comparing the 2018 orbits to past data
The radiant map of that night shows a large concentration of radiants that fail to fulfil the similarity criteria around the Draconid radiant area (Figure 1). The question is why?

Figure 1 – The radiant plot for CAMS BeNeLux, 2018 October 8–9. Radiants that fulfilled the similarity criteria with the 2011 Draconid orbit as reference are marked as blue dots. White dots are sporadics.
For a first identification of Draconid orbits, the reference orbit obtained by CAMS during the 2011 Draconids outburst (Jenniskens et al., 2016) has been used. The reference orbit is presented in Table 1. It should be noted that the 2011 Draconid orbit is only based on a sample of 30 Draconid orbits. This orbit agrees very well with the orbit of the parent comet 21P/Giacobini-Zinner as published by Jenniskens et al. (2016). The Meteor Data Center of the IAU lists a few other reference orbits which can be considered to check the similarity criteria for our 2018 Draconid orbits. The different orbits are listed in Table 2. We also consider the 2018 orbit of the parent comet 21P/Giacobini-Zinner. The results are somehow surprising.
Table 1 – The median values for the reference orbit obtained by CAMS during the Draconid outburst 2011, compared with the orbit of the parent comet.
| DRA (2011) | 21P/G.-Z. (1900) | |
| λʘ | 195° | 195.0° |
| αg | 262.9° | 263.2° |
| δg | +55.7° | +55.8° |
| vg | 20.7 km/s | 20.9 km/s |
| a | 3.15 A.U. | 3.47 A.U. |
| q | 0.996 A.U. | 0.996 A.U. |
| e | 0.706 | 0.707 |
| ω | 173.2° | 173.5° |
| Ω | 195.0° | 195.0° |
| i | 31.4° | 31.8° |
| N | 30 |
The 2011 orbit looks like a valid reference to identify the Draconid orbits among the 1391 orbits registered 8–9 October 2018. A first test shows that 810 of the 1391 orbits fulfil the low threshold similarity criteria with DSH < 0.25 and DD < 0.105 to be Draconid orbits. 572 of these orbits fit the high threshold similarity criteria with DSH < 0.1 and DD < 0.04. Figure 2 shows a close up of the Draconid radiant area in equatorial coordinates. However, 159 orbits which have both their radiant and their velocity within the range to be possible Draconids fail in these similarity criteria. Apparently, the 2011 reference is not the ideal reference to identify all our 2018 Draconid orbits.

Figure 2 – All radiants near the Draconid radiant. Black dots are sporadic radiants, blue dots are low threshold (DSH < 0.25 and DD < 0.105), red are high threshold (DSH < 0.1 and DD < 0.04). 810 orbits fit the low threshold, 572 fit the high threshold.
Table 2 – Draconid orbits as listed by the IAU Meteor Data Center according to different researchers. The orbit of 21P/Giacobini-Zinner given is valid for 2018.
| Gavajdova (1994) | Jenniskens (2006) | Brown et al. (2008) | 21P/G.-Z. (2018) | |
| λʘ | 203.9° | 195.1° | 195.5° | – |
| αg | 274.7° | 264.1° | 261.7° | – |
| δg | +52.4° | +57.6° | +54.8° | – |
| vg | 16.7 km/s | 20.4 km/s | 19.7 km/s | – |
| a | 2.392 A.U. | 3.02 A.U. | 2.89 A.U. | 3.498 A.U. |
| q | 0.995 A.U. | 0.996 A.U. | 0.995 A.U. | 1.0128 A.U. |
| e | 0.584 | 0.670 | 0.656 | 0.71046 |
| ω | 178.2° | 172.9° | 171.9° | 172.86° |
| Ω | 203.9° | 196.4° | 196.6° | 195.39° |
| i | 25.5° | 31.4° | 30.3° | 31.9977° |
| N | 7 | 5 | 20 |
The 1995 reference orbit (Gavajdova, 1994)
Only 329 orbits are detected with the low threshold criterion (DSH < 0.25 and DD < 0.105) and not a single one with the high threshold criterion (DSH < 0.1 and DD < 0.04)! The main problematic element is the ascending node Ω which occurs about a week later than what can be expected for the Draconids. Checking out the original paper it becomes clear that this source should not be listed with the DRA#009 shower in the MDC IAU list. The author searched for shower associations among photographic fireball and bright meteor orbits using only the Southworth and Hawkins criterion with an acceptance of DSH = 0.25. The “October Draconids” mentioned in this paper have nothing to do with the Draconids (DRA#009).
The “October Draconid” orbit published by Gavajdova (1994) has a better match with the delta Cygnids (DCY#282) with DSH = 0.15 and DD = 0.05, a shower discovered by Jenniskens (2006) and believed to be asteroidal in origin. This shower is most likely another instance of the October Cygnids (OCG#083) discovered earlier by Sekanina (1973) which is also similar to the “October Draconids” listed by Gavajdova with DSH = 0.17 and DD = 0.07.
Therefore, we suggest removing this entry from the Draconids (DRA#009) table and rather mention it under the delta Cygnids (DCY#282) together with the October Cygnids (OCG#083).
Jenniskens (2006)
Checking this reference, it is not clear on which data this orbit is based. 780 of our 2018 possible Draconid orbits have a low threshold similarity with this reference, 492 have a high threshold similarity. The 2006 reference orbit fits even less good with our 2018 Draconid orbits than the 2011 reference orbit.
Brown et al. (2008)
This orbit has been based on radar observations mainly obtained during the 2005 outburst. 764 of our 2018 possible Draconid orbits have a low threshold similarity with this reference, 425 have a high threshold similarity. This reference orbit is also not suitable to properly identify all 2018 likely Draconid orbits.
21P/Giacobini-Zinner orbit of 2018
When using the actual parent comet orbit of 2018, we obtain a slightly better fit than with the few older reference orbits we tried so far. 817 of our 2018 possible Draconid orbits have a low threshold similarity with this reference, 566 have a high threshold similarity. But still too many possible Draconid orbits have no similarity with this reference orbit.
3 Different groups of similar orbits?
All attempts failed to derive a single mean orbit which has good similarity to identify all likely 2018 Draconid orbits. All past reference orbits leave a suspect large number of likely Draconids unidentified. Therefore, the question arises if the Draconid stream may consist of a structure with at least two or more groups of similar orbits, different dust trails, which all encounter the Earth at the same descending node, but with slightly different velocities?
The presence of two or more groups of Draconid orbits with a significant difference in eccentricity e, length of perihelion Π or inclination i could explain why a substantial number of the 2018 Draconid orbits fails to fulfill the similarity criteria with a single mean orbit as reference. In this study, we’ll try if we can detect different groups with concentrations of very similar Draconid orbits to explain the failure to fit the similarity criteria for a single mean orbit.
Meteor streams get dispersed along the parent object orbit and gravitational perturbations will result in a considerable spread on orbits. At some point the spread on the orbits will become too large and the D-criteria will fail to confirm any similarity because the orbital elements for differently perturbated segments of the stream differ too much. This complex dynamic evolution of meteor streams is at the basis of different meteor shower complexes. Such complexes cannot be represented with a single reference orbit. In some cases, the planetary perturbations on the orbits must be integrated back in time in order to find a common origin. In our case with the 2018 Draconid orbits all meteors were recorded within a relative short time interval of about 10 hours from the same radiant area at the sky, any differences in some of the orbital elements should be detectable in slightly different radiant positions and slightly faster or slower velocities.
4 A pre-selection of possible Draconids
The idea of this analysis is to search for mean orbits that allow to identify the 2018 Draconids CAMS BeNeLux dataset of Draconid orbits, independently from any previously determined Draconid orbit. For this study we use a slightly adapted version of our iterative method to detect concentrations of similar orbits. This method has been successfully applied in case studies of meteor showers and has been explained in a previous paper (Roggemans et al., 2019).
To calculate a reference orbit for a collection of similar orbits we do not use the median or average values of the orbital elements, but we compute the mean orbit according to the method described by Jopek et al. (2006). To compare orbits on similarity researchers established different discrimination criteria, often abbreviated as D-criteria. The D-criteria that we use are these of Southworth and Hawkins (1963), Drummond (1981) and Jopek (1993) combined. The oldest and most popular D-criterion, the one established by Southworth and Hawkins or DSH proved often too tolerant and unsuitable for short period orbits near the ecliptic. It is not unusual that orbits which are very similar according to DSH, fail for another D-criteria such as that of Drummond or DD.
In order to apply a stricter discrimination, we use three different D-criteria combined to consider five different threshold levels of similarity. The different classes for the threshold are defined as follows:
- Low: DSH < 0.25 & DD < 0.105 & DH < 0.25;
- Medium low: DSH < 0.2 & DD < 0.08 & DH < 0.2;
- Medium high: DSH < 0.15 & DD < 0.06 & DH < 0.15;
- High: DSH < 0.1 & DD < 0.04 & DH < 0.1;
- Very high: DSH < 0.05 & DD < 0.02 & DH < 0.05.
While the low threshold class may contain pure chance similar orbits, the risk for contamination with sporadic orbits is very unlikely for the high and the very high threshold level.

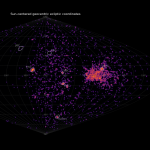
Figure 3 – All the radiants of the 1391 orbits plotted in geocentric Sun-centered ecliptic coordinates as registered by CAMS BeNeLux during the night 2018 October 8–9.
To reduce the number of iterations in our procedure, we remove all orbits which are a priori excluded from being related to the Draconids meteor shower. This pre-selection is normally defined by limiting the activity interval, the radiant and the velocity range. In this particular case the activity interval is just one night. Because the Draconids have their geocentric radiant in Sun centered ecliptic coordinates close to the ecliptic pole (Figure 3) and radiant drift can be neglected in an interval of 10 hours, we will exceptionally use the geocentric equatorial coordinates to select the radiant positions.
To estimate the actual ranges, we use 810 orbits that fit the low threshold class using the 2011 Draconid orbit listed in Table 1 as reference. These 810 orbits occur within the following range in time, radiant and velocity:
- Time interval: 195.176° < λʘ < 195.586°;
- Radiant area: 240° < αg < 276° & +43.5° < δg < +63.4°;
- Velocity: 17 km/s < vg < 24.2 km/s.
For the actual search we set the margins slightly wider in order not to miss any possible Draconids. This way we have a more workable dataset which requires less iterations to detect concentrations of orbits:
- Time interval: 195.14° < λʘ < 195.61°;
- Radiant area: 220° < αg < 360° & +40° < δg < +75°;
- Velocity: 15 km/s < vg < 30 km/s.
The resulting selection includes 969 orbits of the 1391 collected orbits that night. At least 432 orbits were collected that cannot be related to Draconids which is a realistic number of orbits in a single night early October without Draconid activity. Most of the 969 selected orbits must be related to the Draconids, but only 810 at best fit the similarity with the 2011 reference orbit. The 159 other orbits with a radiant and velocity within the above-mentioned ranges are far too many to be all sporadics.
5 Search for orbit concentrations
To locate a first concentration of orbits we calculate the mean orbit for all 969 orbits in our selection, then we compute the D-criteria for each orbit of the selection using this mean orbit as reference orbit. Next, we start the iterative procedure that calculates the average orbit for all orbits that fulfil the low threshold criteria. At each step the D-criteria are recalculated with the new mean orbit as reference until the procedure converges for the low threshold class with a set of orbits that does not change anymore. Then, a new loop of iterations is started using the mean orbit of the very high threshold criterion until convergence is reached. The resulting collection of orbits represents a group of almost identical orbits.
Applying this procedure, we identify several groups of almost identical orbits within our dataset of orbits. The iterative procedure will identify the most dominant group of orbits within the dataset. Once the iteration converges at a selection of almost identical orbits, a mean orbit can be calculated. The orbits that belong to this group are removed from the sample and a new loop of iterations is started to identify the next dominant collection of almost identical orbits. This procedure is repeated until no distinct groupings of orbits can be detected. The procedure confirmed the presence of concentrations or groups of orbits, all sharing the Draconid radiant area but with a wider range in geocentric velocities vg than known before.
Group A: 331 almost identical orbits
After four iterations we have a dataset of orbits with 818 orbits in the low threshold class and 331 orbits in the very high threshold class. We take these 331 orbits apart as these identify a first distinct group of almost identical orbits. Using these 331 orbits for another loop of iterations remains with the same 331 orbits, so it must be a very distinct group of orbits, the crème of our 2018 Draconid orbits. Table 3 lists the mean orbit for these 331 orbits, the standard deviation and the median value of the uncertainties on the individual orbits. The minimum uncertainties on the individual orbits are close to zero and the maximum uncertainties concern only few outliers. These 331 orbits have a median value of DSH = 0.019 and DD = 0.010 which is a very compact concentration, further referred as “Group A”. These orbits have a geocentric velocity vg = 20.8 km/s (median value) with all its geocentric velocities within the range of 19.7 km/s and 22.1 km/s.
Group B: 121 almost identical orbits
In order to locate a possible next group of very similar orbits, we remove the first 331 orbits of group A and repeat our iterative procedure on the remaining dataset with 638 candidate Draconid orbits. After five iterations the procedure converges with a stable number of 491 orbits that fulfil the low threshold level, 31 of which fulfil the very high threshold level. Using the mean orbit for these 31 very similar orbits as reference (DD < 0.02), after few iterations we find 121 orbits which fit the very high threshold D-criteria which determine a second group of very similar orbits (Table 4). These 121 orbits have a median value of DSH = 0.020 and DD = 0.010 which is also a very compact concentration. The Draconids in group B have a geocentric velocity vg = 21.7 km/s (median value) with all its geocentric velocities within the range of 21.7 km/s and 22.8 km/s. Group B may be regarded as a slightly faster component than Group A.
Group C: 170 almost identical orbits
We remove the 121 very similar orbits of group B and repeat the iterative procedure on the remaining 517 orbits until the iteration converges for the low threshold similarity class. The procedure ends with 355 low threshold orbits of which 84 orbits fulfil the very high threshold criteria. Using the mean orbit for these 84 very similar orbits as reference, few more iterations result in a third group with 170 almost identical orbits (Table 5). These 170 orbits have a median value of DSH = 0.016 and DD = 0.008 another very compact concentration. The Draconids in group C have a geocentric velocity vg = 20.2 km/s (median value) with all its geocentric velocities within the range of 18.8 km/s and 21.1 km/s, a slightly slower component than group A.
Group D: 45 almost identical orbits
Removing the 170 orbits of the group C leaves 347 possible Draconid orbits to search. The same procedure is applied as for previous groups. The result is a small but very distinct group of 45 orbits of orbits with higher eccentricity and higher inclination (Table 6). This group of orbits appears remarkably compact with very small values for DD and DSH. Because of the eccentricity e, these orbits are missing among the first 810 Draconid orbits identified with the 2011 reference orbit given by Jenniskens et al. (2016). These 45 orbits have a median value of DSH = 0.023 and DD = 0.010, a very compact concentration situated well beyond the main Draconid stream. The Draconids in group D have a geocentric velocity vg = 24.2 km/s (median value) with all its geocentric velocities within the range of 23.4 km/s and 25.4 km/s which well above the past reference values.
Group E: 58 almost identical orbits
The next loop through the 302 remaining orbits required six iterations on the low threshold class and eight on the very high threshold class to detect another group with 58 very similar orbits (Table 7). These 58 orbits have a median value of DSH = 0.024 and DD = 0.011. The Draconids in group E have a geocentric velocity vg = 22.7 km/s (median value) with all its geocentric velocities within the range of 21.5 km/s and 23.9 km/s. Group E is the fifth and last distinct group of very high threshold orbits that we can locate in our dataset.
For the remaining 244 orbits we make the iteration loop converge in the high threshold class with DSH < 0.1 and DD = 0.04 instead of the very high threshold class in order to locate groups with significant numbers of orbits with a slightly less compact concentration than previous five groups.
Group F: 28 orbits with high eccentricity
The next loop on 244 remaining orbits ends after nineteen iterations with 28 orbits with all a remarkable high value for the eccentricity e (Table 8). These 28 orbits have a median value of DSH = 0.039 and DD = 0.016. This group is likely connected to group D with its high eccentricity orbits. Although the error margin on the velocities measured by CAMS are reasonably small, the presence of 11 slightly hyperbolic cases among these 28 orbits indicates measurement inaccuracies. However, the number of so many high eccentricity orbits cannot entirely be explained by just measuring errors. The Draconids in group F have a geocentric velocity vg = 25.4 km/s (median value) with all its geocentric velocities within the range of 24.3 km/s and 26.5 km/s. Group F can be considered as a component related to group D with slightly faster Draconids and more dispersed orbits.
Group G: 69 orbits with low eccentricity
At this point the dataset has 216 orbits left. After fourteen iterations on the low threshold class and four more iterations on the high threshold class the procedure converges on a group of 69 orbits that fit the high threshold similarity, 45 orbits of these even fit the very high threshold class. This group is close to group C and has the smallest eccentricity of all groups (Table 9). These 69 orbits have a median value of DSH = 0.031 and DD = 0.015. The Draconids in group G have a geocentric velocity vg = 19.6 km/s (median value) with all its geocentric velocities within the range of 17.1 km/s and 22.4 km/s. Group G looks related to group C, containing more dispersed and slower Draconids.
Group H: 24 very similar orbits
The 147 orbits left in this procedure allowed a last iteration loop to converge at a group of 24 orbits fitting the high threshold similarity. This group resembles much to group E except for a difference of 1° in both inclination i and length of perihelion Π. These 24 orbits have a median value of DSH = 0.047 and DD = 0.021. The Draconids in group H have a geocentric velocity vg = 22.6 km/s (median value) with all its geocentric velocities within the range of 20.3 km/s and 24.2 km/s.
The final remaining 123 orbits include 40 hyperbolic cases which were most likely affected by measuring inaccuracies. Most of the remaining orbits are dispersed Draconids with medium or low threshold similarity with one or more of the above listed groups. Some orbits differ too much in length of perihelion and are likely sporadics. No further groupings of orbits can be detected in this remaining dataset.
Table 3 – Group A. The mean orbit for the first group of 331 almost identical Draconid orbits which fulfil the very high threshold class with DD < 0.02 for the orbit mentioned.
| Mean orbit |
S.D. | Median uncertainty | Max. uncertainty | |
| λʘ | 195.38° | ±0.08° | – | – |
| αg | 262.5° | ±1.0° | ±0.5° | ±5.6° |
| δg | +55.9° | ±0.8° | ±0.2° | ±2.5° |
| vg | 20.8 km/s | ±0.4 | ±0.07 | ±0.8 |
| λ-λʘ | 52.7° | ±2.7° | ±1.2° | ±10.5° |
| β | +78.7° | ±0.8° | ±0.3° | ±2.5° |
| a | 3.42 AU | ±0.18 | – | – |
| q | 0.9958 AU | ±0.0007 | ±0.0003 | ±0.008 |
| e | 0.7088 | ±0.01 | ±0.007 | ±0.06 |
| ω | 172.98° | ±0.8° | ±0.3° | ±4.7° |
| Ω | 195.37° | ±0.08° | – | – |
| i | 31.7° | ±0.6° | ±0.1° | ±1.0° |
| Π | 8.4° | ±0.8° | ±0.3° | ±4.7° |
| Q | 5.75 AU | ±0.35 | – | – |
| Tj | 2.52 | ±0.08 | – | – |
| P | 6.2 y | ±0.5 | – | – |
| N | 331 |
Table 4 – Group B. The mean orbit for the second group with 121 almost identical Draconid orbits which fulfil the very high threshold class with DD < 0.02 for the orbit mentioned.
| Mean orbit |
S.D. | Median uncertainty | Max. uncertainty | |
| λʘ | 195.38° | ±0.08° | – | – |
| αg | 262.9° | ±1.2° | ±0.6° | ±5.4° |
| δg | +56.1° | ±0.9° | ±0.3° | ±2.0° |
| vg | 21.7 km/s | ±0.4 | ±0.09 | ±0.9 |
| λ-λʘ | 53.3° | ±3.6° | ±1.4° | ±15.6° |
| β | +79.0° | ±0.9° | ±0.3° | ±2.0° |
| a | 4.10 AU | ±0.24 | – | – |
| q | 0.9961 AU | ±0.0008 | ±0.0003 | ±0.004 |
| e | 0.7568 | ±0.01 | ±0.008 | ±0.07 |
| ω | 173.47° | ±0.9° | ±0.4° | ±4.0° |
| Ω | 195.37° | ±0.08° | – | – |
| i | 32.8° | ±0.7° | ±0.1° | ±1.1° |
| Π | 8.8° | ±0.9° | ±0.4° | ±4.0° |
| Q | 7.18 AU | ±0.49 | – | – |
| Tj | 2.25 | ±0.07 | – | – |
| P | 8.3 y | ±0.7 | – | – |
| N | 121 |
Table 5 – Group C. The mean orbit for the third group with 170 almost identical Draconid orbits which fulfil the very high threshold class with DD < 0.02 for the orbit mentioned.
| Mean orbit |
S.D. | Median uncertainty | Max. uncertainty | |
| λʘ | 195.37° | ±0.07° | – | – |
| αg | 262.1° | ±1.3° | ±0.7° | ±6.1° |
| δg | +55.8° | ±0.9° | ±0.4° | ±2.5° |
| vg | 20.2 km/s | ±0.4 | ±0.08 | ±0.8 |
| λ-λʘ | 51.6° | ±3.5° | ±1.8° | ±12.1° |
| β | +78.6° | ±0.9° | ±0.4° | ±2.4° |
| a | 2.98 AU | ±0.10 | – | – |
| q | 0.9956 AU | ±0.0010 | ±0.0005 | ±0.009 |
| e | 0.6664 | ±0.01 | ±0.010 | ±0.06 |
| ω | 172.57° | ±1.0° | ±0.5° | ±5.3° |
| Ω | 195.37° | ±0.07° | – | – |
| i | 31.0° | ±0.7° | ±0.2° | ±1.0° |
| Π | 7.9° | ±1.1 | ±0.5° | ±5.3° |
| Q | 5.00 AU | ±0.19 | – | – |
| Tj | 2.70 | ±0.06 | – | – |
| P | 5.2 y | ±0.3 | – | – |
| N | 170 |
Table 6 – Group D. The mean orbit for the fourth group with 45 almost identical Draconid orbits which fulfil the very high threshold class with DD < 0.02 for the orbit mentioned.
| Mean orbit |
S.D. | Median uncertainty | Max. uncertainty | |
| λʘ | 195.36° | ±0.08° | – | – |
| αg | 263.8° | ±1.0° | ±0.6° | ±5.5° |
| δg | +56.5° | ±0.8° | ±0.3° | ±1.5° |
| vg | 24.2 km/s | ±0.4 | ±0.11 | ±0.8 |
| λ-λʘ | 55.5° | ±3.2° | ±1.8° | ±16.1° |
| β | +79.4° | ±0.8° | ±0.3° | ±1.6° |
| a | 10.3 AU | ±2.2 | – | – |
| q | 0.9965 AU | ±0.0006 | ±0.0004 | ±0.004 |
| e | 0.9034 | ±0.02 | ±0.012 | ±0.08 |
| ω | 174.20° | ±0.7° | ±0.4° | ±3.7° |
| Ω | 195.35° | ±0.08° | – | – |
| i | 35.4° | ±0.7° | ±0.2° | ±1.2° |
| Π | 9.4° | ±0.8° | ±0.4° | ±3.7° |
| Q | 19.6 AU | ±4.5 | – | – |
| Tj | 1.48 | ±0.10 | – | – |
| P | 33.1 y | ±11.2 | – | – |
| N | 45 |
Table 7 – Group E. The mean orbit for the fifth group with 58 almost identical Draconid orbits which fulfil the very high threshold class with DD < 0.02 for the orbit mentioned.
| Mean orbit |
S.D. | Median uncertainty | Max. uncertainty | |
| λʘ | 195.36° | ±0.07° | – | – |
| αg | 263.2° | ±1.3° | ±1.0° | ±7.2° |
| δg | +56.3° | ±1.0° | ±0.4° | ±2.0° |
| vg | 22.7 km/s | ±0.5 | ±0.15 | ±1.1 |
| λ-λʘ | 54.2° | ±4.0° | ±3.0° | ±18.3° |
| β | +79.2° | ±1.0° | ±0.4° | ±3.0° |
| a | 5.4 AU | ±0.5 | – | – |
| q | 0.9962 AU | ±0.0008 | ±0.0006 | ±0.01 |
| e | 0.8143 | ±0.02 | ±0.015 | ±0.09 |
| ω | 173.76° | ±1.0° | ±0.7° | ±5.2° |
| Ω | 195.36° | ±0.07° | – | – |
| i | 33.9° | ±0.8° | ±0.2° | ±1.4° |
| Π | 9.0° | ±1.0° | ±0.7° | ±5.2° |
| Q | 9.62 AU | ±1.03 | – | – |
| Tj | 1.96 | ±0.09 | – | – |
| P | 12.2 y | ±1.8 | – | – |
| N | 58 |
Table 8 – Group F. The mean orbit for the sixth group with 28 almost identical Draconid orbits which fulfil the high threshold class with DD < 0.04 for the orbit mentioned.
| Mean orbit |
S.D. | Median uncertainty | Max. uncertainty | |
| λʘ | 195.36° | ±0.08° | – | – |
| αg | 263.9° | ±1.8° | ±0.7° | ±4.5° |
| δg | +56.6° | ±1.2° | ±0.4° | ±1.4° |
| vg | 25.4 km/s | ±0.6 | ±0.14 | ±0.65 |
| λ-λʘ | 55.5° | ±5.2° | ±2.2° | ±13.9° |
| β | +79.6° | ±1.2° | ±0.4° | ±1.5° |
| a | 80 AU | ±94 | – | – |
| q | 0.9965 AU | ±0.001 | ±0.0004 | ±0.003 |
| e | 0.9876 | ±0.03 | ±0.015 | ±0.07 |
| ω | 174.43° | ±1.3° | ±0.4° | ±2.8° |
| Ω | 195.34° | ±0.08° | – | – |
| i | 36.6° | ±0.9° | ±0.2° | ±0.9° |
| Π | 9.6° | ±1.3° | ±0.4° | ±2.8° |
| Q | 129 AU | – | – | – |
| Tj | 1.10 | – | – | – |
| P | 527 y | – | – | – |
| N | 28 |
Table 9 – Group G. The mean orbit for the seventh group with 69 almost identical Draconid orbits which fulfil the high threshold class with DD < 0.04 for the orbit mentioned.
| Mean orbit |
S.D. | Median uncertainty | Max. uncertainty | |
| λʘ | 195.37° | ±0.06° | – | – |
| αg | 261.5° | ±3.6° | ±0.9° | ±8.5° |
| δg | +56.3° | ±2.2° | ±0.6° | ±3.2° |
| vg | 19.6 km/s | ±0.9 | ±0.13 | ±0.88 |
| λ-λʘ | 49.7° | ±10.7° | ±2.4° | ±18.4° |
| β | +78.9° | ±2.3° | ±0.7° | ±3.3° |
| a | 2.64 AU | ±0.12 | – | – |
| q | 0.9946 AU | ±0.003 | ±0.0008 | ±0.01 |
| e | 0.6226 | ±0.02 | ±0.016 | ±0.08 |
| ω | 172.29° | ±2.9° | ±0.8° | ±7.5° |
| Ω | 195.36° | ±0.06° | – | – |
| i | 30.8° | ±1.8° | ±0.3° | ±1.3° |
| Π | 7.9° | ±2.9 | ±0.8° | ±7.5° |
| Q | 4.33 AU | ±0.23 | – | – |
| Tj | 2.91 | ±0.09 | – | – |
| P | 4.4 y | ±0.3 | – | – |
| N | 69 |
Table 10 – Group H. The mean orbit for the eighth group with 24 almost identical Draconid orbits which fulfil the high threshold class with DD < 0.04 for the orbit mentioned.
| Mean orbit |
S.D. | Median uncertainty | Max. uncertainty | |
| λʘ | 195.37° | ±0.07° | – | – |
| αg | 263.3° | ±3.8° | ±1.1° | ±4.4° |
| δg | +54.2° | ±1.9° | ±0.5° | ±2.0° |
| vg | 22.6 km/s | ±1.0 | ±0.17 | ±0.69 |
| λ-λʘ | 55.1° | ±9.8° | ±0.2° | ±0.7° |
| β | +77.0° | ±2.0° | ±0.5° | ±2.0° |
| a | 6.00 AU | ±1.12 | – | – |
| q | 0.9944 AU | ±0.003 | ±0.0008 | ±0.003 |
| e | 0.8341 | ±0.03 | ±0.015 | ±0.07 |
| ω | 172.73° | ±2.8° | ±0.8° | ±2.9° |
| Ω | 195.37° | ±0.07° | – | – |
| i | 32.9° | ±1.7° | ±0.3° | ±1.0° |
| Π | 8.9° | ±2.8° | ±0.8° | ±2.9° |
| Q | 11.94 AU | ±2.23 | – | – |
| Tj | 1.81 | ±0.16 | – | – |
| P | 16.4 y | ±4.2 | – | – |
| N | 24 |
Using these groups as reference orbit
The eight compact concentrations of Draconid orbits were used as a range of reference orbits to check all 1391 orbits obtained during this night on possible similarity with the mean orbits of each of the eight groups. In total 938 orbits fulfill the similarity criteria with at least one of the mean orbits of the eight groups. Table 11 lists the number of orbits counted for each group for each class of similarity threshold. Note that the groups with the highest velocities (D and F) have the smallest numbers of positive matches.
Table 11 – Number of orbits that match with the mean orbit of a group counted for each similarity threshold class (Lo = low; Ml = medium low; Mh = medium high, H = high and Vh = very high).
| A | B | C | D | E | F | G | H | |
| Lo | 814 | 839 | 775 | 324 | 762 | 172 | 697 | 684 |
| Ml | 764 | 739 | 716 | 199 | 525 | 118 | 570 | 411 |
| Mh | 693 | 613 | 635 | 131 | 312 | 84 | 402 | 245 |
| H | 568 | 378 | 491 | 81 | 160 | 51 | 183 | 126 |
| Vh | 331 | 155 | 243 | 45 | 60 | 18 | 55 | 43 |
Most orbits fulfill the similarity criteria for more than one group. In fact, only four orbits match with a single mean orbit. All four have low values for the eccentricity e, 0.516 to 0.540 with low and medium low similarity with the mean orbit of group G (with the slowest geocentric velocity). Ten orbits match with two different groups, 27 with three of the groups, 122 with four different groups, 137 with five different groups, 490 with six different groups and 111 with seven different groups but not any single orbit satisfies similarity with all eight groups. Table 12 lists the number of orbits that each group has in common with another group with the groups ordered from slow to fast.
Table 12 – The number of orbits that a group has in common with each of the eight groups. The cross sections of each group marked in bold is the total number of orbits associated with this group.
| G | C | A | B | E | H | D | F | |
| G | 697 | 693 | 686 | 660 | 562 | 476 | 97 | 0 |
| C | 693 | 775 | 768 | 742 | 642 | 557 | 177 | 14 |
| A | 686 | 768 | 814 | 788 | 688 | 603 | 222 | 59 |
| B | 660 | 742 | 788 | 839 | 739 | 654 | 273 | 110 |
| E | 562 | 642 | 688 | 739 | 762 | 676 | 296 | 133 |
| H | 476 | 557 | 603 | 654 | 676 | 684 | 303 | 140 |
| D | 97 | 177 | 222 | 273 | 296 | 303 | 324 | 161 |
| F | 0 | 14 | 59 | 110 | 133 | 140 | 161 | 172 |
Table 13 – Number of orbits that match with the reference orbit from different literature sources, counted for each similarity threshold class (Lo = low; Ml = medium low; Mh = medium high, H = high and Vh = very high).
| Reference orbit | Lo | Ml | Mh | H | Vh |
| Gavajdova (1994) | 325 | 70 | 2 | 0 | 0 |
| Jenniskens (2006) | 780 | 721 | 639 | 492 | 257 |
| Brown et al. (2008) | 764 | 687 | 598 | 425 | 179 |
| Jenniskens et al. (2016) | 810 | 763 | 694 | 572 | 340 |
| 21P/Giacobini-Zinner | 817 | 765 | 692 | 566 | 297 |
Table 14 – Mean orbit for 938 Draconid orbits identified according to the range of mean orbits of the 8 groups of Draconid orbits.
| Mean orbit |
S.D. | Minimum value | Maximum value | |
| λʘ | 195.37° | ±0.07° | 195.146° | 195.586° |
| αg | 262.7° | ±3.1° | 240.1° | 281.0° |
| δg | +56.0° | ±1.8° | +43.5° | +67.7° |
| vg | 20.9 km/s | ±1.8 | 15.8 km/s | 31.1 km/s |
| λ-λʘ | 53.0° | ±15.4° | 8.6° | 351.8° |
| β | +78.8° | ±1.9° | +64.7° | +86.7° |
| a | 3.82 AU | – | – | – |
| q | 0.9937 AU | ±0.003 | 0.96196 | 0.9991 |
| e | 0.73988 | ±0.105 | 0.5163 | 1.18 |
| ω | 173.165° | ±2.46° | 155.181° | 185.155° |
| Ω | 195.349° | ±0.07° | 195.147° | 195.588° |
| i | 32.37° | ±2.14° | 23.77° | 47.53° |
| Π | 8.514° | ±2.46° | 350.605° | 20.578° |
| Q | 6.65 AU | – | – | – |
| Tj | 2.34 | – | – | – |
| P | 7.47 y | – | – | – |
| N | 938 |
Checking our 938 Draconid orbits with past reference orbits (see Table 1 and Table 2), using any of these reference orbits misses a significant number of our 938 Draconid orbits. Table 13 lists the number of orbits in each threshold class of similarity that fits the criteria for each of the reference orbits listed. The reference given by Jenniskens et al. (2016), based on the 2011 Draconid return, as well as the 2018 orbit of the parent comet 21P/Giacobini-Zinner are the best matching references, but both still fail to identify about 15% of all the candidate Draconid orbits.
The mean orbit for all 938 Draconids is listed in Table 14 together with the standard deviation, for completeness we also mention the outliers with the highest and lowest value for each parameter where applicable.
The more than 120 obvious Draconid orbits that fail to be identified as Draconids when using just a single valid reference orbit to check similarity, mostly concern orbits with a remarkable fast heliocentric velocity vh, including 37 with a hyperbolic orbit which must be due to velocity measuring inaccuracies. The problem concerns mainly group F and to a less extent group D.
Velocity measurement uncertainties are a typical problem for high velocity meteors such as Leonids, Orionids and Perseids. It is a bit a mystery how this could affect slow meteors like the Draconids with geocentric velocities typically within the range of 19 to 22 km/s. 24% of our 938 Draconids have geocentric velocities faster than 22 km/s which is a strong indication that the shower may include a component which encounters the Earth at a slightly higher velocity than the main Draconid stream, assuming that the velocity measurements in the CAMS system are correct. The error margins calculated by the CAMS software are rather small and cannot explain the excess in remarkable fast Draconids. The remarkable high velocities found from the CAMS BeNeLux data remains without confirmation from other studies. Question is how Draconids were identified in other studies? The most common approach for known meteor showers is to use a past orbit as reference or to simply select meteors based on the known radiant position and velocity, ignoring all outliers. However, this is a rather biased way to identify shower members as the reference values of the past are assumed to be representative for any future returns. Any changes in the stream structure will remain unnoticed this way.
The remarkable number of “too fast” Draconids requires further investigations which we discuss in Section 9.
6 Activity profile
The number of Draconid orbits counted in time bins of 15 minutes offers a reasonably good possibility to reconstruct an activity profile. To temper statistical fluctuations, we count the number of orbits in time bins of 0.02° in solar longitude, shifted 0.01° at each step. The radiant elevation varies greatly during the night. When observations started the Draconid radiant was at about 80° elevation for the center of the CAMS BeNeLux network. When the shower display was in full progress at 22h UT, the radiant was at 45° getting at 17° by the end of the display. Since the radiant elevation within the network was about the same for all cameras, a zenith distance correction can be applied similar to ZHR calculations. We apply this correction to the number of orbits counted in each time bin for the zenith distance Z with a factor sec(Z).

Figure 4 – The number of orbits counted in bins of 0.02° duration shifted per 0.01° solar longitude for each group of similar orbits as described in Section 5, corrected for zenith distance.

Figure 5 – The number of orbits counted in bins of 0.02° duration shifted per 0.01° solar longitude for all 938 Draconid orbits, corrected for zenith distance.
Figure 4 shows the activity profile with different colors for the different concentrations of orbits. The groups are ordered from slow at the bottom to fast at the top layers. The two groups, D and F, with the somehow problematic high velocities represent rather small numbers. The profile shows a “shoulder” around λʘ = 195.25° (20h27m UTC), the main peak occurred at 195.35° < λʘ < 195.38° (22h53m to 23h36m UTC) followed by another peak at λʘ = 195.41° (0h20m UTC). The activity profile is skew with a steeper ascending branch and a slower descending branch. Another sub-maximum appeared at λʘ = 195.47° (1h48m UTC). The time of the best activity agrees well with the prediction of Maslov (2011), who predicted 23h to 0h UTC, but the actual activity was much higher than expected. Ye et al. (2013) predicted the peak at λʘ = 195.4° (0h06m UTC). The results can be compared with the visual observations analyzed by Miskotte (2019). Nothing unusual was detected at λʘ = 195.25° in the visual data, but too few visual data was available at this time. The visual data had a fairly flat maximum during 195.34° < λʘ < 195.40°, no sub-maximum at λʘ = 195.41° but at λʘ = 195.44°, although all this varies within the error margins. The visual data has also a sub-maximum at λʘ = 195.48° (Miskotte, 2019).
Using all our 938 Draconid orbits does not change much to the shape of the activity profile (Figure 5). Although we corrected the number of Draconid orbits for the zenith distance, these profiles are no ZHR profiles. The sky conditions are not taken into account. For a relatively small camera network in a single night we can assume that the number of non-shower orbits has the same sky condition influence as the number of shower orbits. If we express the shower activity as a percentage relative to the non-shower activity, we can eliminate the effect of sky conditions. However, for network data from a limited geographical area, the random statistical fluctuations of non-shower activity for each time interval and the effect of the diurnal variation will seriously distort the shower activity profile. The effect of the diurnal variation on the proportion Draconids/sporadics will result in an overestimation in the evening hours and an underestimation in the morning hours. This is what we see in Figure 6. Here the peak at λʘ = 195.25° stands out while the maximum interval during 195.34° < λʘ < 195.40° gets a bit deformed because of a sudden increase in sporadics at λʘ [195.36°–195.37°]. The sub-maximum at λʘ = 195.48° remains well visible although the level will be underestimated due to the diurnal variation effect.

Figure 6 – Number of Draconid orbits expressed as a percentage relative to the number of non-Draconid orbits in the same time bin.
These activity profiles show the main features but should be regarded with caution because these are based on raw counts. Both Vida et al. (2020) and Koten et al. (2014) reported a very rapid change in the population index which was observed in the Draconid returns of 2011 and 2018. Miskotte (2019) found a variable population index for the 2018 Draconids, but not the sudden and strong variation found by Vida et al. (2020). The most likely explanation is that not enough visual magnitude data were available for short observing intervals. Unfortunately, the magnitude data of the CAMS BeNeLux Draconids were not available for analyzing.
If we consider Draconids identified on a single reference orbit, instead of our range of orbits the activity profile and its features remain unchanged (Figure 7).

Figure 7 – The number of orbits counted in bins of 0.02° duration shifted per 0.01° solar longitude for all 817 Draconid orbits identified with the 2018 21P/Giacobini-Zinner orbit, with the number of orbits corrected for zenith distance.
7 The Draconid radiant
Would the concentrations of orbits be visible in the radiant of the Draconids? Apart from some outliers, the Draconids radiate from a rather compact radiant area. Plotting the radiants in geocentric equatorial coordinates the large number of radiants results in a crowded picture with overlapping radiant points between the different groups. Therefore, we plot two versions with all radiants plotted in layers, once with the fast velocity radiants in front (Figure 8) and once with the slow velocity radiants in front (Figure 9). The slower velocity radiants appear mainly towards the bottom-left quarter and the faster velocity radiants in the upper right quarter of the radiant area.

Figure 8 – Radiants plotted in geocentric equatorial coordinates. The Draconid groups are plotted in layers with the slow velocity radiants (G) in the background and the fast in front (F).

Figure 9 – Radiants plotted in geocentric equatorial coordinates. The Draconid groups are plotted in layers with the fast velocity radiants (F) in the background and the slow in front (G).

Figure 10 – The radiant positions for the 938 Draconid orbits in Sun centered geocentric ecliptic coordinates with the geocentric velocity marked color coded.

Figure 11 – The radiant positions in Sun centered geocentric ecliptic coordinates for the median value of each group of Draconid orbits with the s.d. as error bars.
Looking at the radiant plot in Sun-centered geocentric ecliptic coordinates does not really help to see the general picture because of the scatter of the radiant points being close to the ecliptic pole (Figure 10). Plotting the median values for the Sun centered geocentric ecliptic coordinates for each group reveals a trend for the groups C, A, B, Z, D and F as the values of λg – λʘ and βg increase with higher geocentric velocities vg. Groups G and H have a much larger spread than the other groups (Figure 11).

Figure 12 – The inclination i in function of the length of perihelion Π with the geocentric velocity vg color coded.

Figure 13 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits, plotted in layers with the slow velocity orbits in the background and the fast in front.

Figure 14 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits, plotted in layers with the fast velocity orbits in the background and the slow in front.
Plotting the inclination i against the length of perihelion Π with the geocentric velocity vg color coded displays a clear trend with the higher inclination orbits having a higher velocity (Figure 12). The same plot of i against Π, but for the groups with concentrations of similar orbits shows the same pattern. The ‘slow’ orbits appear in the bottom left part, the ‘fast’ orbits in the upper right part. The groups were plotted in layers, once with the ‘fast’ orbits in front (Figure 13) and once with the ‘slow’ orbits in front (Figure 14).
In Figures 15 to 28 we compare the plots for seven different time intervals. For each time bin we show the plot based on all Draconids, including the outliers with a color code for the geocentric velocity, compared with the plot of the orbits that fulfill the very high threshold similarity criteria for each of the groups with a concentration of orbits. Groups A to E appear very compact while F, G and H appear more dispersed. The strength of each group in each time bin changes but these changes can be explained as statistical fluctuations. It seems that all the groups and the entire velocity range was registered during the entire activity period, but some groups appear absent in some intervals.

Figure 15 – The inclination i in function of the length of perihelion Π with the geocentric velocity vg color coded for the interval λʘ < 192.21°.

Figure 16 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits for the interval λʘ < 192.21°.

Figure 17 – The inclination i in function of the length of perihelion Π with the geocentric velocity vg color coded for the interval 195.21° < λʘ < 192.29°.

Figure 18 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits for the interval 195.21° < λʘ < 192.29°.

Figure 19 – The inclination i in function of the length of perihelion Π with the geocentric velocity vg color coded for the interval 195.29° < λʘ < 192.34°.

Figure 20 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits for the interval 195.29° < λʘ < 192.34°.

Figure 21 – The inclination i in function of the length of perihelion Π with the geocentric velocity vg color coded for the interval 195.34° < λʘ < 192.40°.

Figure 22 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits for the interval 195.34° < λʘ < 192.40°.

Figure 23 – The inclination i in function of the length of perihelion Π with the geocentric velocity vg color coded for the interval 195.40° < λʘ < 192.45°.

Figure 24 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits for the interval 195.40° < λʘ < 192.45°.

Figure 25 – The inclination i in function of the length of perihelion Π with the geocentric velocity vg color coded for the interval 195.45° < λʘ < 192.50°.

Figure 26 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits for the interval 195.45° < λʘ < 192.50°.

Figure 27 – The inclination i in function of the length of perihelion Π with the geocentric velocity vg color coded for the interval 195.50° < λʘ < 192.60°.

Figure 28 – The inclination i in function of the length of perihelion Π for the different groups of high threshold similarity orbits for the interval 195.50° < λʘ < 192.60°.
8 The heliocentric orbits
In Section 5 we screened our dataset of orbits to locate concentrations of Draconid orbits. Using the range of mean orbits for the detected groups of very similar orbits we could identify 938 Draconid orbits. However, this approach includes orbits with suspicious fast Draconids with velocities well above the common values in literature. If we use a more conventional way to identify Draconid orbits, a significant number of radiant points is left that fail to fit the similarity criteria, mainly because of the velocity.
If we use the 21P/Giacobini-Zinner orbit for the comet’s 2018 return as a reference orbit, 817 orbits fulfill the low threshold similarity criteria. 121 of our 938 orbits fail, mainly because of too high velocities. We can compare both results for some of the orbital parameters. Looking at some parameters:
Eccentricity e: The mean orbit has e = 0.7399 ± 0.105 (median value e = 0.7102 ± 0.105) for the 938 orbits and e = 0.7112 ± 0.056 (median value e = 0.7033 ± 0.056) for the 817 orbits. The histogram of the different eccentricity values is identical for the common part. The only difference between Figure 29 and Figure 30 are the outliers with higher eccentricities which don’t fit the similarity criteria for the 21P/Giacobini-Zinner orbit as reference. Gajdoš et al. (2020) found e = 0.7026 ± 0.0367. Koten et al. (2020) has e = 0.712.

Figure 29 – Histogram showing the eccentricity distribution for all 938 Draconid orbits identified by the groups, counted in 0.01 bins.

Figure 30 – Histogram showing the eccentricity distribution for all 817 Draconid orbits identified by using the 2018 orbit of 21P/Giacobini-Zinner as reference orbit, counted in 0.01 bins.
Inclination i: The mean orbit has i = 32.37° ± 2.14° (median value i = 31.84° ± 2.14°) for the 938 orbits and i = 31.85° ± 1.38° ° (median value i = 31.69° ± 1.38°) for the 817 orbits. The main part of the histograms in Figure 31 and Figure 32 is identical. Gajdoš et al. (2020) found i = 31.55° ± 0.77°. Koten et al. (2020) has i = 31.88°.

Figure 31 – Histogram showing the inclination distribution for all 938 Draconid orbits identified by the groups, counted in 0.2° bins.

Figure 32 – Histogram showing the inclination distribution for all 817 Draconid orbits identified by using the 2018 orbit of 21P/Giacobini-Zinner as reference orbit, counted in 0.2° bins.
Semi major axis a: The mean orbit has a = 3.82 A.U. and the median value for all 938 orbits is a = 3.44 A.U. (Figure 33). For the 817 orbits identified with the 2018 orbit for 21P/Giacobini-Zinner, we find a = 3.45 A.U. for the mean orbit and the median value for these orbits is a = 3.36 A.U. (Figure 34). Gajdoš et al. (2020) found a = 3.40 ± 0.41 A.U. Koten et al. (2020) has a = 3.46 A.U.

Figure 33 – Histogram showing the semi major axis distribution for all 938 Draconid orbits identified by the groups, counted in 0.1 A.U. bins.

Figure 34 – Histogram showing the semi major axis distribution for all 817 Draconid orbits identified by using the 2018 orbit of 21P/Giacobini-Zinner as reference orbit, counted in 0.1 A.U. bins.
Perihelion distance q: The mean orbit has q = 0.9937 A.U. while the median value for all 938 orbits is q = 0.9961 ± 0.003 A.U. (Figure 35). Looking at the 817 orbits identified with the 2018 orbit for 21P/Giacobini-Zinner, q = 0.9951 A.U. for the mean orbit and the median value for these orbits is q = 0.9960 ± 0.003 A.U. (Figure 36). Gajdoš et al. (2020) found q = 0.9963 ± 0.0007 A.U. Koten et al. (2020) has q = 0.9960 A.U.

Figure 35 – Histogram showing the perihelion distance distribution for all 938 Draconid orbits identified by the groups, counted in 0.001 A.U. bins.

Figure 36 – Histogram showing the perihelion distance distribution for all 817 Draconid orbits identified by using the 2018 orbit of 21P/Giacobini-Zinner as reference orbit, counted in 0.001 A.U. bins.
Length of perihelion Π: The mean orbit has Π = 8.51° ± 2.46° for the 938 orbits and a median value of Π = 8.49° ± 2.46°. The mean orbit for the 817 orbits has Π = 8.28° ± 2.19°, the median value is Π = 8.41° ± 2.19°. Also, here, the main part of the histograms in Figure 37 and Figure 38 is identical. Gajdoš et al. (2020) found Π = 8.75° ± 0.85°. Koten et al. (2020) has Π = 8.41°.

Figure 37 – Histogram showing the length of perihelion distribution for all 938 Draconid orbits identified by the groups, counted in 0.1° bins.

Figure 38 – Histogram showing the length of perihelion distribution for all 817 Draconid orbits identified by using the 2018 orbit of 21P/Giacobini-Zinner as reference orbit, counted in 0.1° bins.
9 Geocentric velocities
The initial challenge of this analysis was to explain why we had so many, more than 100, multi-station events with a concentration at the Draconid radiant that failed to be confirmed as a Draconid meteor when using a classic single reference orbit to verify the similarity. Most researchers identify shower meteors using known radiant position, velocity and orbit from previous research, as did we in section 2. Our alternative approach was to search for concentrations of orbits without considering past established Draconid orbits. This has been done with an algorithm based on an iterative loop to locate narrow concentrations of orbits. The Draconid meteor shower is obviously a complex mixture of dust trails left by different perihelion passages of the parent comet. The different concentrations we found cannot be linked to any perihelion passage related dust trail. The groups of almost identical orbits defined by our iterative loop mainly split the Draconids up in bins with similar radiant-velocity combinations. Most remarkably, some concentrations are well above the literature values for the geocentric velocity known for the Draconids. The first most evident explanation is that some measurement artifact affected the velocities, however the error margins on the measured velocities by the CAMS software exclude that any systematic artifact could cause erroneous velocity measurements.

Figure 39 – Distribution of the geocentric velocities for all 938 Draconid orbits identified by the groups. The black line is the linear regression fit.

Figure 40 – Distribution of the geocentric velocities for all 817 Draconid orbits identified by using the 2018 orbit of 21P/Giacobini-Zinner as reference orbit. The black line is the linear regression fit.
Not all multiple station events produce a favorable triangulation. Such cases are rejected on the basis of a rigid quality assessment. Unfortunately, the author had no access to the trajectory data. A separate investigation focused on the remarkable fast Draconids may shed some light on this phenomenon, looking at the trajectory lengths, duration measurements etc. In 2019 a number of CAMS operators reported so-called “Zebrids”, meteor trails on which a number of frames were skipped during the detection. This artifact did not affect all cameras, only those working with a problematic configuration. For instance, when 20 fps occurred on a meteor trail while the system assumes 25 fps such 20% discrepancy can explain why the duration is underestimated and the velocity overestimated. A meteor with an actual velocity of 20 km/s ends up with an erroneous velocity of 25 km/s. According to the personal comments by the CAMS BeNeLux network coordinator, Carl Johannink, such cases are rejected and as far as the author knows, such cases did not occur during the Draconids.
Draconids are very slow meteors, slow meteors are not very sensitive to instrumental measurement errors. Assuming that the CAMS velocity derivation is reliable, there should be another explanation for the groups of similar Draconids with higher velocities than expected. The existence of one or more dust trails with faster particles could be an explanation. Other studies may have simply ignored these orbits if they had these too, assuming these weren’t Draconids because of the speed. The velocity mainly determines the semi major axis a, the eccentricity e and to less extent the inclination i. For this reason, the orbits of these faster ‘Draconids’ with higher eccentricity and higher inclination will fail in the similarity criteria. If we simply assume that these ‘too’ fast Draconids must be ignored, we risk to bias the picture.
Comparing the geocentric velocity distribution in function of the solar longitude (Figure 39) and the histogram (Figure 41) for the 938 Draconids with the 817 Draconids identified with the 2018 orbit of 21P/Giacobini-Zinner as reference orbit (Figures 40 and 42), the only difference between both are the outliers. The median value for all 938 orbits is vg = 20.91 ± 1.78 km/s. Looking at the 817 orbits identified with the 2018 orbit for 21P/Giacobini-Zinner, the median value for these orbits is vg = 20.79± 1.01 km/s. Vida et al. (2020) found a mean geocentric velocity of 20.05 ± 0.93 km/s, Gajdoš et al. (2020) found 20.71 ± 0.66 km/s, Koten et al. (2020) found 20.96 km/s.
Both the histograms with the geocentric velocity and the histograms for the orbital elements aren’t smooth profiles but show some sub-peaks that correspond with the median values for some of the different groups of Draconid orbits obtained in Section 5. This could be an indication for the presence of dust trails each with slightly different orbital elements.

Figure 41 – Histogram of the geocentric velocities for all 938 Draconid orbits identified by the groups (0.1 km/s bins).

Figure 42 – Histogram of the geocentric velocities for all 817 Draconid orbits identified by using the 2018 orbit of 21P/Giacobini-Zinner as reference orbit (0.1 km/s bins).
10 Conclusion
Applying the method to detect orbit concentrations on the dataset with possible Draconid orbits of 2018 allowed to resolve five distinct groups of very similar Draconid orbits and three slightly more dispersed groups. The velocity range covered by these groups include orbits with geocentric velocities higher than the traditional values published in literature. The range in velocities is displayed in the radiant structure, in the plots of the inclination versus length of perihelion as well as in the histograms of the orbital elements. The activity profile based on the number of orbits counted within bins of 0.02° in solar longitude shows the main peak activity as well as some sub-maxima. None of these maxima can be related to any specific group of orbits. The different groups can be seen at slightly different positions within the radiant structure, as well as in the distributions of the geocentric velocities and the orbital elements. This could be an indication for the presence of different dust trails with slightly different velocity and orbits.
The method used to identify the Draconid meteors, using a range of mean orbits or using a single reference orbit, only influences the total number of Draconids but has no influence on the activity profile, radiant structure or any other aspect of the results.
Acknowledgment
The author thanks Denis Vida for making the Python script available to compute mean orbits and for plotting color coded distributions. The author also thanks CAMS BeNeLux coordinator, Carl Johannink, for making the orbit data for 2018 October 8–9 available for this analysis. Thanks also to all the camera operators. The CAMS BeNeLux team is operated by the following volunteers: Hans Betlem (Leiden, CAMS 371, 372 and 373), Jean-Marie Biets (Wilderen, CAMS 380, 381 and 382), Martin Breukers (Hengelo, CAMS 320, 321, 322, 323, 324, 325, 326, 327, 328 and 329), Bart Dessoy (Zoersel, CAMS 397, 398, 804, 805 and 806), Jean-Paul Dumoulin / Christian Wanlin (Grapfontaine, CAMS 814, 815), Luc Gobin (Mechelen, CAMS 390, 391, 807 and 808), Tioga Gulon (Nancy, France, CAMS 3900 and 3901), Robert Haas (Alphen aan de Rijn, CAMS 3160, 3161, 3162, 3163, 3164, 3165, 3166 and 3167), Robert Haas / Edwin van Dijk (Burlage, CAMS 801, 802, 821 and 822), Robert Haas (Texel, CAMS 810, 811, 812 and 813), Klaas Jobse (Oostkapelle, CAMS 3030, 3031, 3032, 3033, 3034, 3035, 3036 and 3037), Carl Johannink (Gronau, CAMS 311, 312, 313, 314, 315, 316, 317 and 318), Hervé Lamy (Ukkel, CAMS 393), Koen Miskotte (Ermelo, CAMS 351, 352, 353 and 354), Piet Neels (Terschelling, CAMS 841, 842, 843 and 844), Tim Polfliet (Gent, CAMS 396), Steve Rau (Zillebeke, CAMS 3850 and 3852), Paul Roggemans (Mechelen, CAMS 383, 384, 388, 389, 399 and 809), Hans Schremmer (Niederkruechten, CAMS 803), Erwin van Ballegoij (CAMS 347 and 348) and Marco Van der Weide (CAMS 3110).
References
Brown P.; Weryk R. J.; Wong D. K.; Jones J. (2008). “A meteoroid stream survey using the Canadian Meteor Orbit Radar. I. Methodology and radiant catalogue”. Icarus, 195, 317–339.
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Egal A., Wiegert P., Brown P.G., Moser D. E., Moorhead A. V. and Cooke W.J. (2018). “The Draconid meteoroid stream 2018: prospects for satellite impact detection”. The Astrophysical Journal Letters, 866, Issue 1, article id L.8, 8 pages. https://arxiv.org/pdf/1809.07393.pdf.
Gajdoš Š., Tóth J., Kornoš L. (2020). “October Draconids 2018 outburst by AMOS”. Planetary and Space Science, 184, 104995.
Gavajdova M. (1994). “On the population of very bright meteors in meteor streams”. Contributions of the Astronomical Observatory Skalnate Pleso, 24, 101–110.
Jenniskens P. (2006). Meteor Showers and their Parent Comets, ISBN 0521853494. Cambridge, UK: Cambridge University Press.
Jenniskens P., Gural P. S., Grigsby B., Dynneson L., Koop M. and Holman D. (2011). “CAMS: Cameras for All-sky Meteor Surveillance to validate minor meteor showers”. Icarus, 216, 40–61.
Jenniskens P., Nénon Q., Albers J., Gural P. S., Haberman B., Holman D., Morales R., Grigsby B. J., Samuels D. and Johannink C. (2016). “The established meteor showers as observed by CAMS”. Icarus, 266, 331–354.
Johannink C. (2018). “Draconid outburst observed October 8th 2018 by CAMS BeNeLux”. eMetN, 3, 296–297.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Jopek T. J., Rudawska R. and Pretka-Ziomek H. (2006). “Calculation of the mean orbit of a meteoroid stream”. Monthly Notices of the Royal Astronomical Society, 371, 1367–1372.
Koten P., Vaubaillon J., Tóth J., Margonis A., Ďuriš F. (2014). “Three Peaks of 2011 Draconid Activity Including that Connected with Pre-1900 Material”. Earth Moon and Planets, 112, 15–31.
Koten P., Borovička J., Vojáček V., Spurný P., Rostislav Štork R., Shrbený L., Janout P., Fliegel K., Páta P., Vítek S. (2020). “Activity profile, mass distribution index, radiants, and orbits of the 2018 Draconid meteor shower outburst”. Planetary and Space Science, 184, 104871.
Martin P. (2019). “Observation October 8-9, 2018 Draconids outburst from Indiana, U.S.A.”. eMetN, 4, 14–20.
Maslov M. (2011). “Future Draconid outbursts (2011 – 2100)”. WGN, Journal of the International Meteor Organization, 39, 64–67.
Miskotte K. (2019a). “The outburst of the Draconid meteor shower in 2018: an analysis”. eMetN, 4, 74–78.
Miskotte K. (2019b). “Draconid observations 8–9 October 2018”. eMetN, 4, 89–90.
Roggemans P. (2018). “First impressions of the 2018 Draconids outburst”. eMetN, 3, 293–295.
Roggemans P., Johannink C. and Cambell-Burns P. (2019). “October Ursae Majorids (OCU#333)”. eMetN, 4, 55–64.
Sekanina Z. (1973). “Statistical Model of Meteor Streams. III. Stream Search Among 19303 Radio Meteors”. Icarus, 18, 253–284.
Southworth R. R. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithson. Contrib. Astrophys., 7, 261–286.
Vida D., Merlak A. and Segon D. (2018). “2018 Draconids as seen by low-cost RPI based meteor camera”. eMetN, 3, 298–299.
Vida D., Campbell-Brown M., Brown P. G., Egal A., and Mazur M. J. (2020). “A new method for measuring the meteor mass index: application to the 2018 Draconid meteor shower outburst”. Astronomy & Astrophysics, 635, id. A153, 16 pp.
Ye Q., Wiegert P. A., Brown P. G., Campbell-Brown M. D., and Weryk R. J. (2014). “The Unexpected 2012 Draconid Meteor Storm”. Monthly Notices of the Royal Astronomical Society, 437, 3812–3823.