By Damir Šegon, Denis Vida and Paul Roggemans
Abstract: A new meteor shower on a Long-period comet type orbit (TJ = –0.22) has been detected during July 25 – August 3, 2025 by the Global Meteor Network. Meteors belonging to the new shower were observed between 122° < λʘ < 131° from a radiant at R.A. = 29.5° and Decl.= –21.1° in the constellation of Eridanus, with a geocentric velocity of 61.4 km/s. The new meteor shower has been listed in the Working List of Meteor Showers under the temporary name-designation: M2025-P1.
Introduction
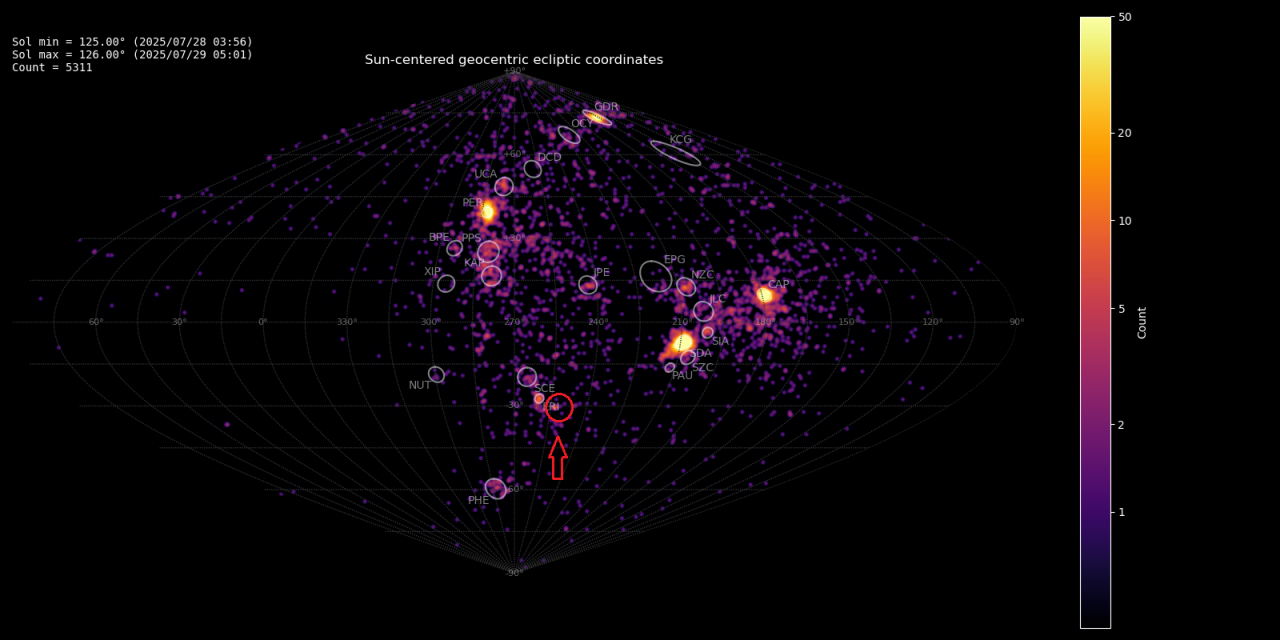
The GMN radiant map for July 28–29, 2025 shows a weak concentration of related radiants in the constellation of Eridanus not far from the established shower, eta Eridanids (ERI#191). 32 meteors of this meteor shower were observed by the Global Meteor Network low-light video cameras on 2025 July 25 – August 3 with most events on July 28–29 (Figure 1). The shower was independently observed by cameras in six countries (Australia, Brazil, Greece, South Korea, New Zealand and the United States).
The shower had a median geocentric radiant with coordinates R.A. = 29.5°, Decl. = –21.1°, within a circle with a standard deviation of ±1.1° (equinox J2000.0) see Figure 2. The radiant drift in R.A. is +0.79 deg on the sky per degree of solar longitude and +0.56 in Dec., both referenced to λʘ = 125.6° (Figures 3 and 4). The median Sun-centered ecliptic coordinates were λ – λʘ = 253.3°,
β = –30.9° (Figure 5). The geocentric velocity was 61.4 ± 0.2 km/s.
This possible new meteor shower was reported to the IAU MDC and added under the temporary identification 2025-P1.
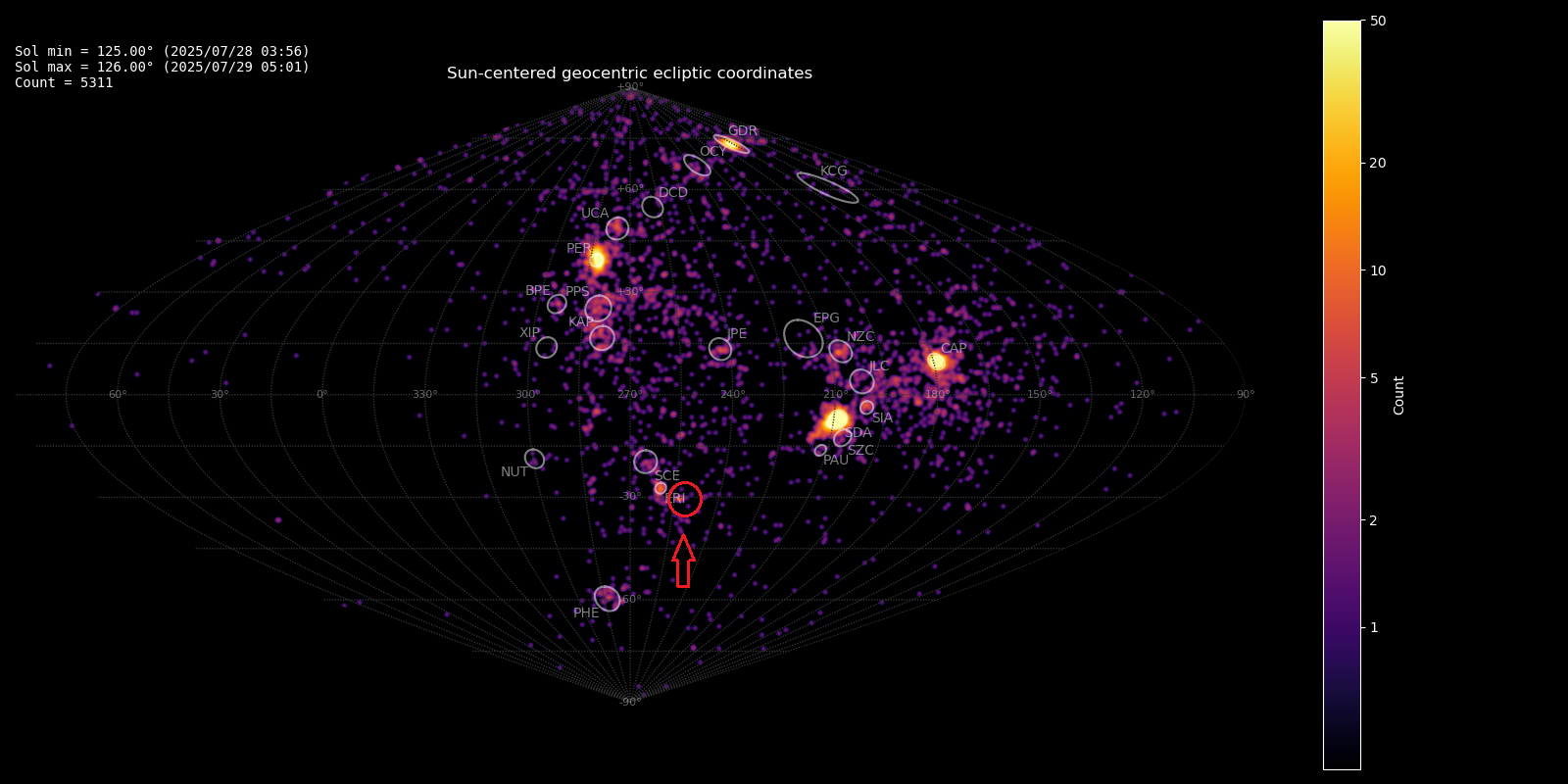
Figure 1 – Heat map with 5311 radiants obtained by the Global Meteor network on July 28–29 2025. A weak concentration is visible in Sun-centered geocentric ecliptic coordinates which was identified as a new meteor shower with the temporary identification M2025-P1.
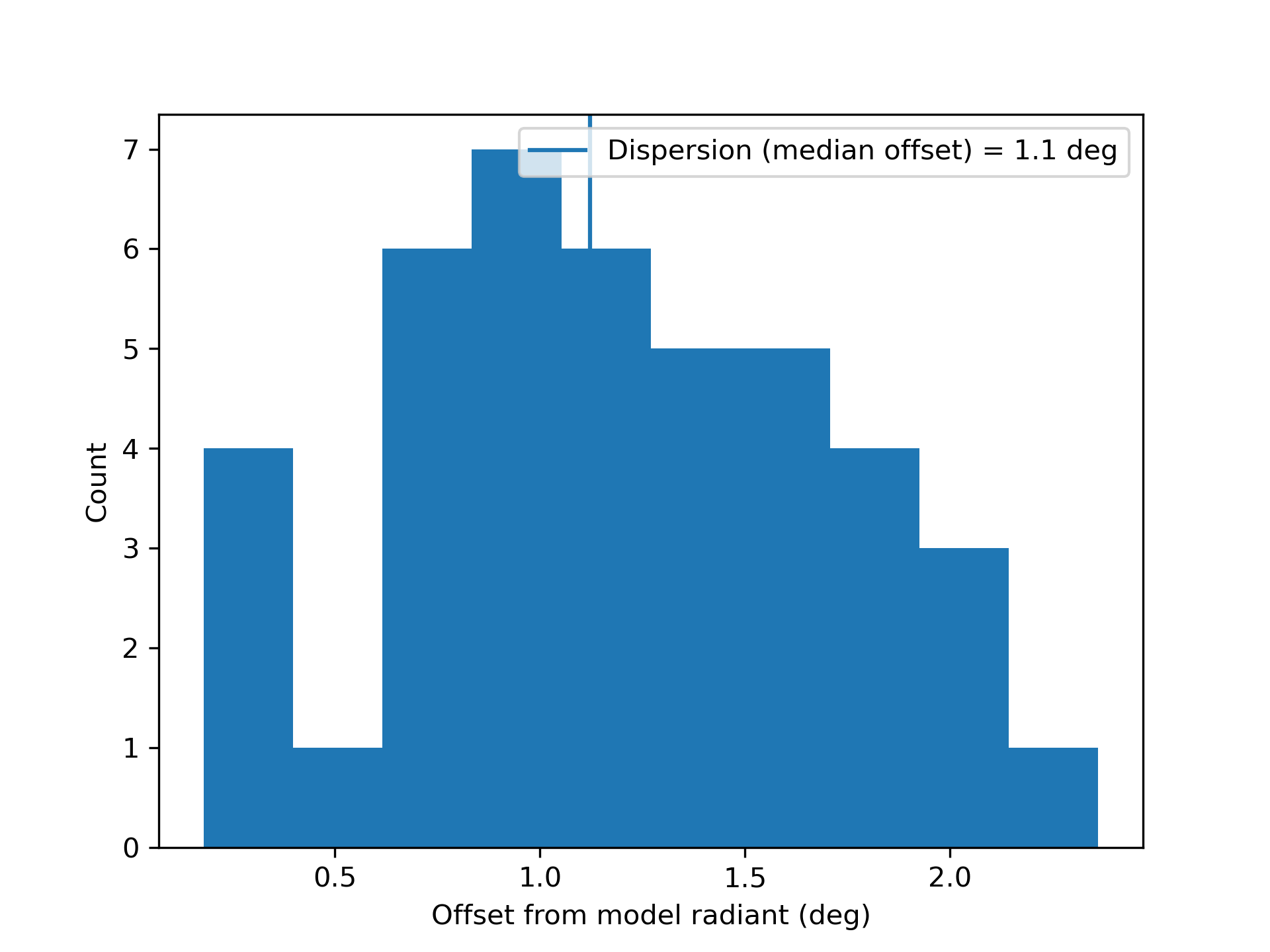
Figure 2 – Dispersion on the radiant position.
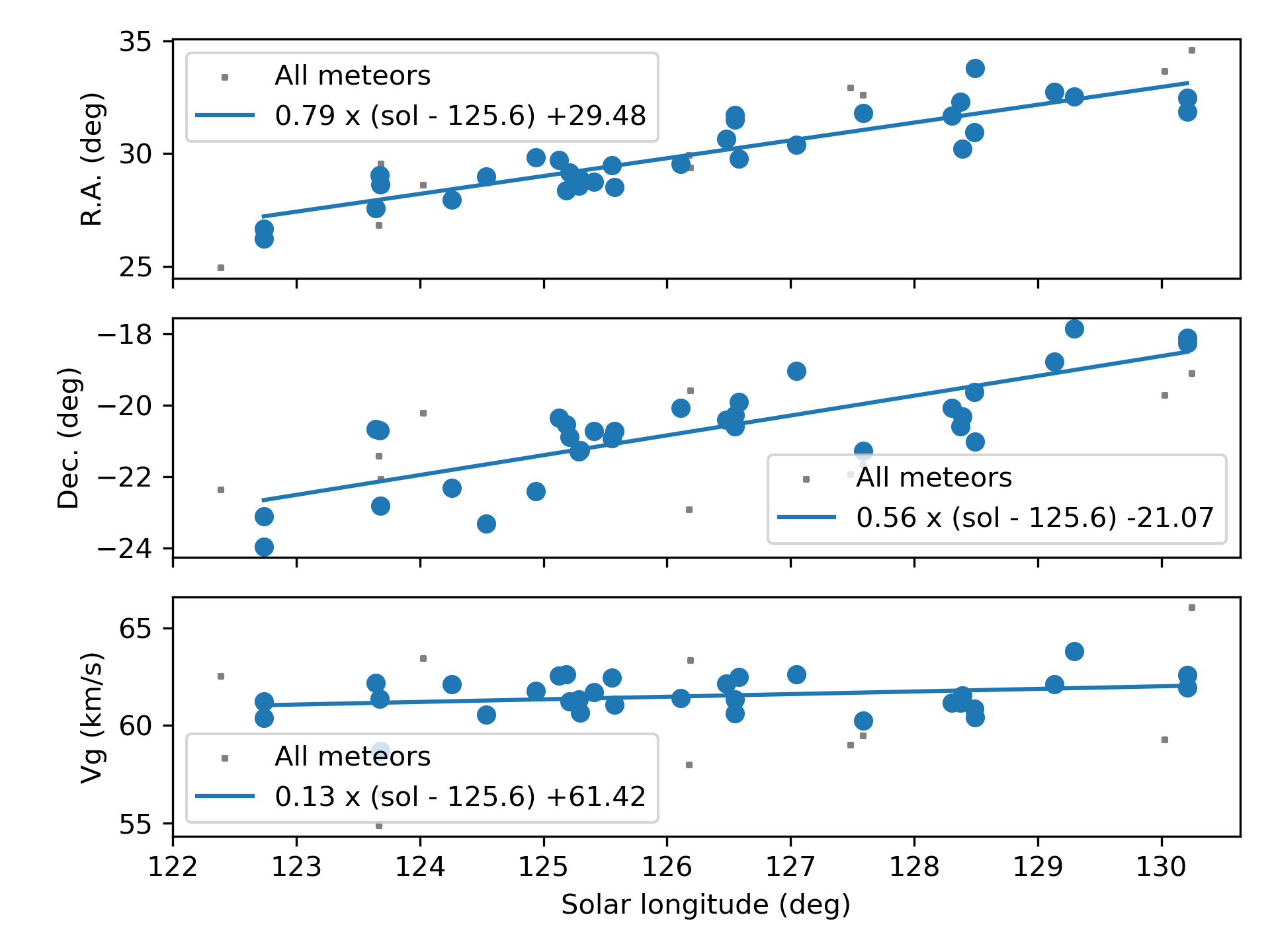
Figure 3 – The radiant drift.
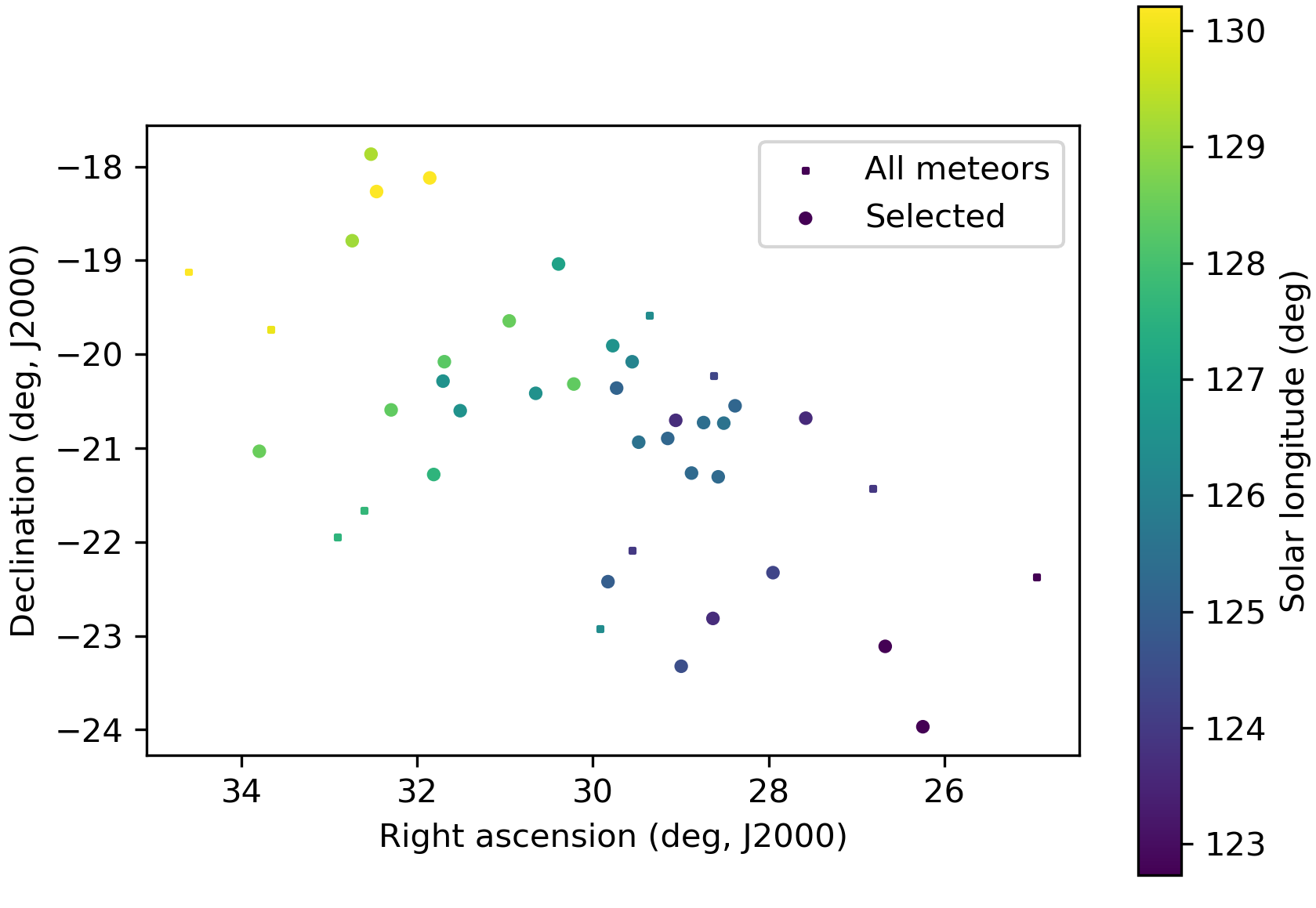
Figure 4 – The radiant distribution during the solar-longitude interval 122° – 131° in equatorial coordinates.
First detection
The GMN shower association criterion assumes that meteors within 1° in solar longitude, within 3° in radiant, and within 10% in geocentric velocity of a shower reference location are members of that shower. Further details about the shower association are explained in Moorhead et al. (2020). This is a rather strict criterion since meteor showers often have a larger dispersion in radiant position, velocity and activity period. Using these meteor shower selection criteria, 32 orbits have been associated with the new shower in the GMN meteor orbit database and the mean orbit has been listed in Table 1.
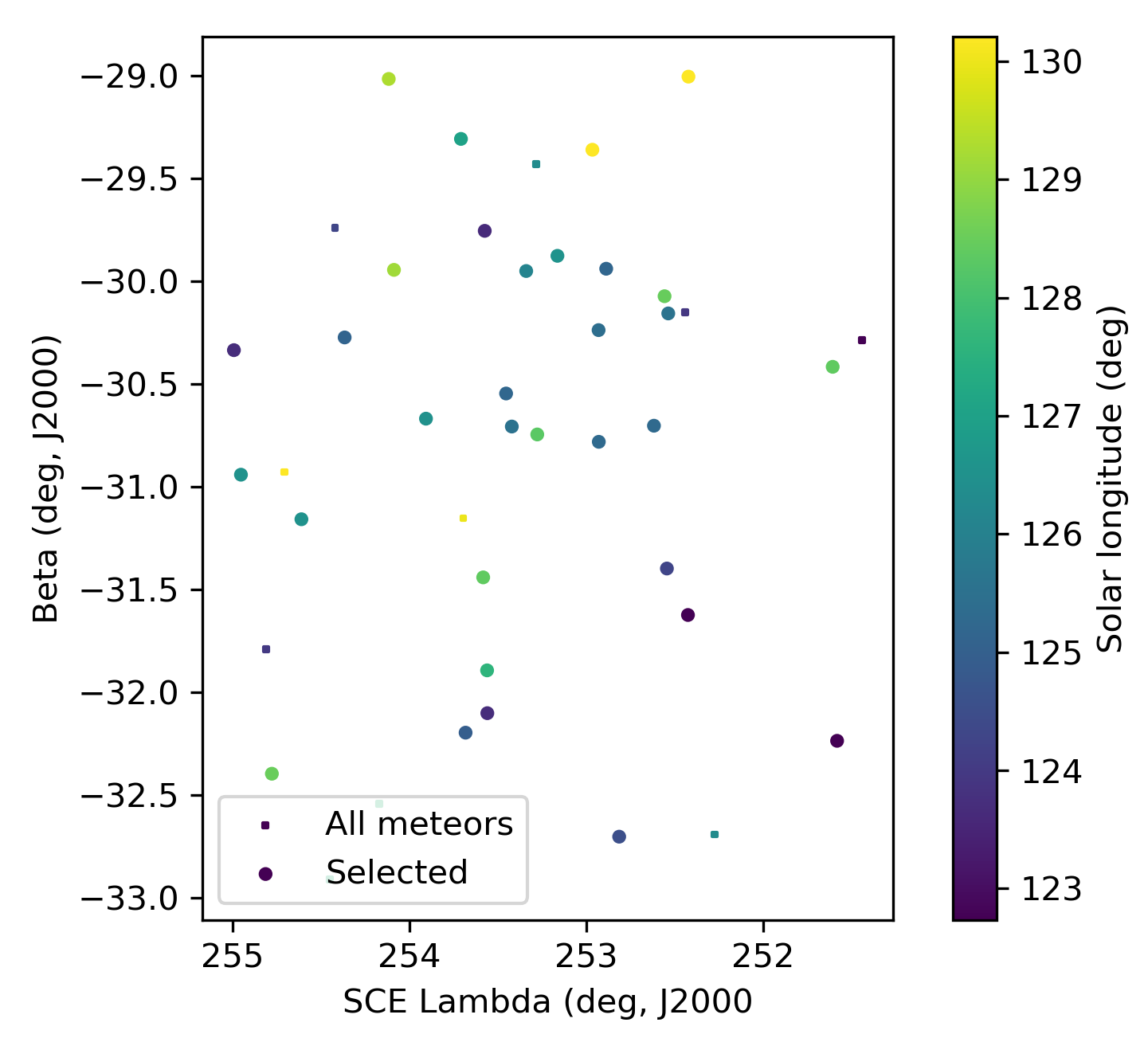
Figure 5 – The radiant distribution during the solar-longitude interval 122° – 131° in Sun centered geocentric ecliptic coordinates.
Another search method
Another method has been applied to check this new meteor shower discovery. The starting point here can be any visually spotted concentration of radiant points or any other indication for the occurrence of similar orbits. The method has been described before (Roggemans et al., 2019). The main difference with the method applied in Section 2 is that three different discrimination criteria are combined in order to have only those orbits which fit different criteria. The D-criteria that we use are these of Southworth and Hawkins (1963), Drummond (1981) and Jopek (1993) combined. Instead of using a cutoff value for the threshold of the D-criteria these values are considered in different classes with different thresholds of similarity. Depending on the dispersion and the type of orbits, the most appropriate threshold of similarity is selected to locate the best fitting mean orbit as the result of an iterative procedure.
This method resulted in a mean orbit with 89 related orbits that fit within the similarity threshold with DSH < 0.20, DD < 0.08 and DJ < 0.20, recorded 2025 July 25 – August 3. The plot of the radiant positions in equatorial coordinates, color coded for different D-criteria thresholds, shows a stretched trail in Right Ascension from about 25° to 35° due to the radiant drift (Figure 6), see also Figure 3.
Looking at the Sun-centered geocentric ecliptic coordinates the radiant drift caused by of the Earth moving on its orbit around the Sun is compensated and a more compact radiant becomes visible (Figure 7). The blue dots with DSH < 0.25, DD < 0.105 and DJ < 0.25 as well as the green dots with DSH < 0.20, DD < 0.08 and DJ < 0.20 display a large dispersion and may include some contamination with sporadics and outliers belonging to the nearby eta Eridanids (ERI#191). To reduce the risk of including these orbits, in the second method only the 27 orbits that fit the threshold with DSH < 0.10, DD < 0.05 and DJ < 0.10 are considered.
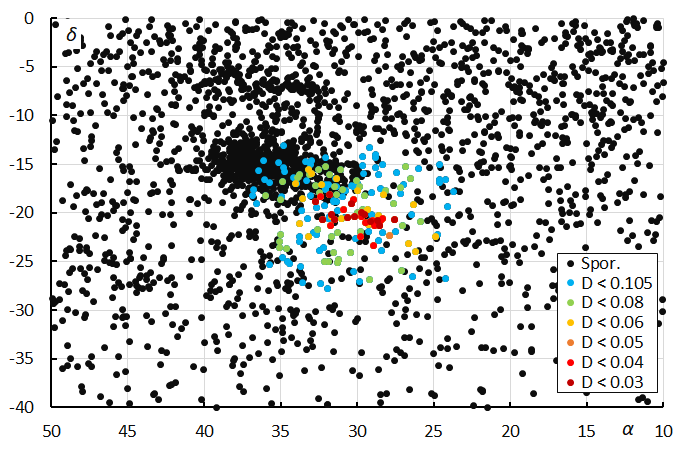
Figure 6 – The radiant distribution during the solar-longitude interval 122° – 131° in equatorial coordinates, color coded for different values of the DD orbit similarity criterion.
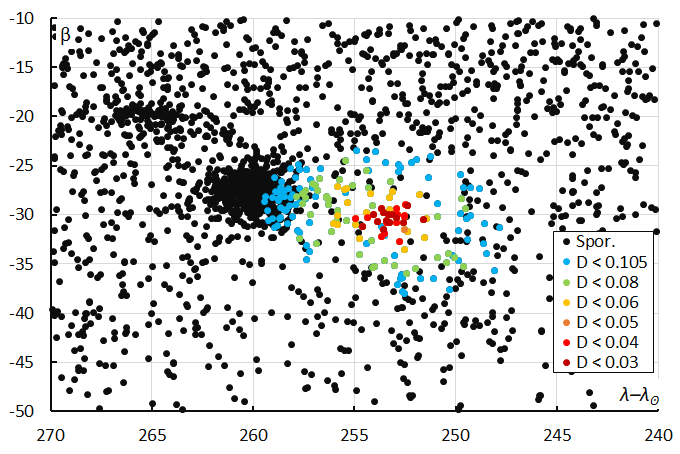
Figure 7 – The radiant distribution during the solar-longitude interval 122° – 131° in Sun-centered geocentric ecliptic coordinates, color coded for different values of the DD orbit similarity criterion.
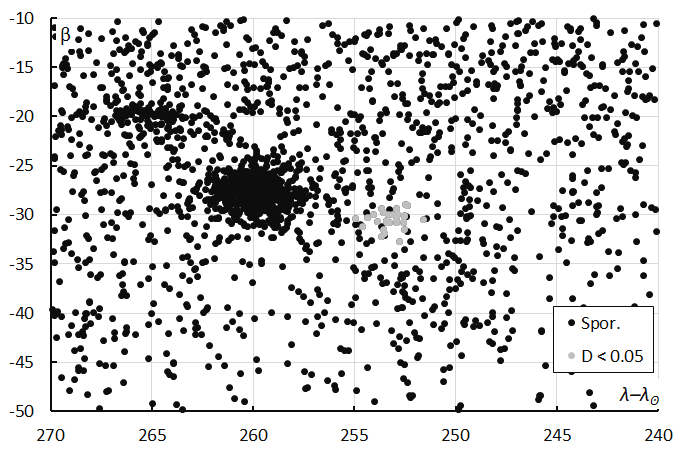
Figure 8 – The sporadic radiants during the solar-longitude interval 122° – 131° in Sun-centered geocentric ecliptic coordinates, with M2025-P1 radiants marked in grey for DD < 0.05.
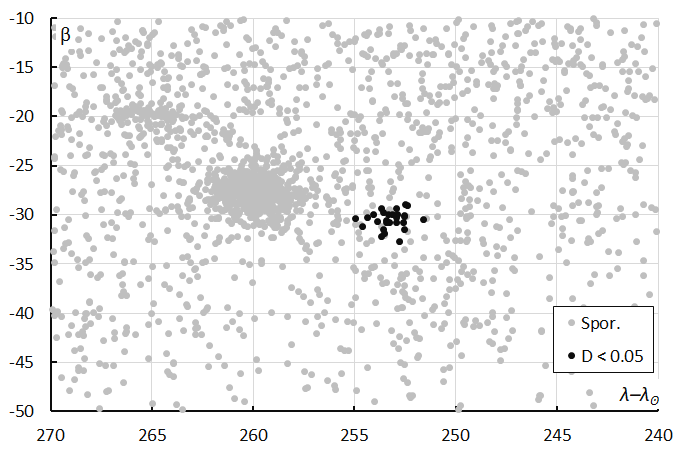
Figure 9 – The M2025-P1 radiants for DD < 0.05 during the solar-longitude interval 122° – 131° in Sun-centered geocentric ecliptic coordinates, with the sporadic radiants marked in grey.
Figures 8 and 9 show that these radiants appear on top of an evenly distributed sporadic radiant background. The other concentration of radiants visible left of M2025-P1 in Figures 7, 8 and 9 belong to the eta Eridanids (ERI#191). Left above the eta Eridanids another concentration is visible, which are radiants of the 77-Cetids (SCE#1070) which looks like a duplicate of the rho Eridanids (RER#738), both reported by Jenniskens (2024). The presence of these other sources nearby M2025-P1 is a likely explanation why M2025-P1 remained unnoticed so far.
The diagram with the inclination against the longitude of perihelion (Figure 10) shows quite a lot dispersion on the longitude of perihelion Π.
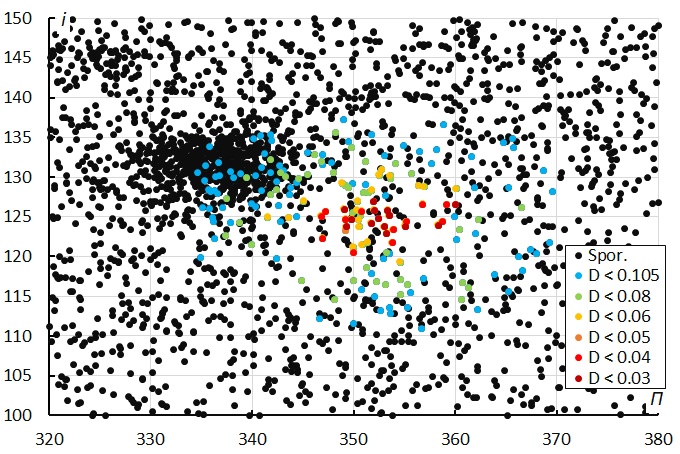
Figure 10 – The diagram of the inclination i against the longitude of perihelion Π color coded for different classes of D criterion threshold.
Orbit and parent body
The final mean orbits obtained by the two methods are almost identical (Figure 11, Table 1). The orbit of the eta Eridanids has been included to show that this is a very different orbit than M2025-P1. Figure 12 shows the orbits in the inner solar system. The dust of M2025-P1 crosses the Earth orbit at its ascending node, hitting the Earth almost head-on from below the ecliptic plane.
Only one orbit of the 32 meteors identified as M2025-P1 by the first shower identification fails to fit the DSH < 0.20, DD < 0.08 and DJ < 0.2 threshold. Six meteors identified by the first method were not used in the second method because they fail to fit the DSH < 0.10, DD < 0.05 and DJ < 0.10 threshold. Only one orbit (20250731142527_hG3bc) identified by the second method was ignored by the first method.
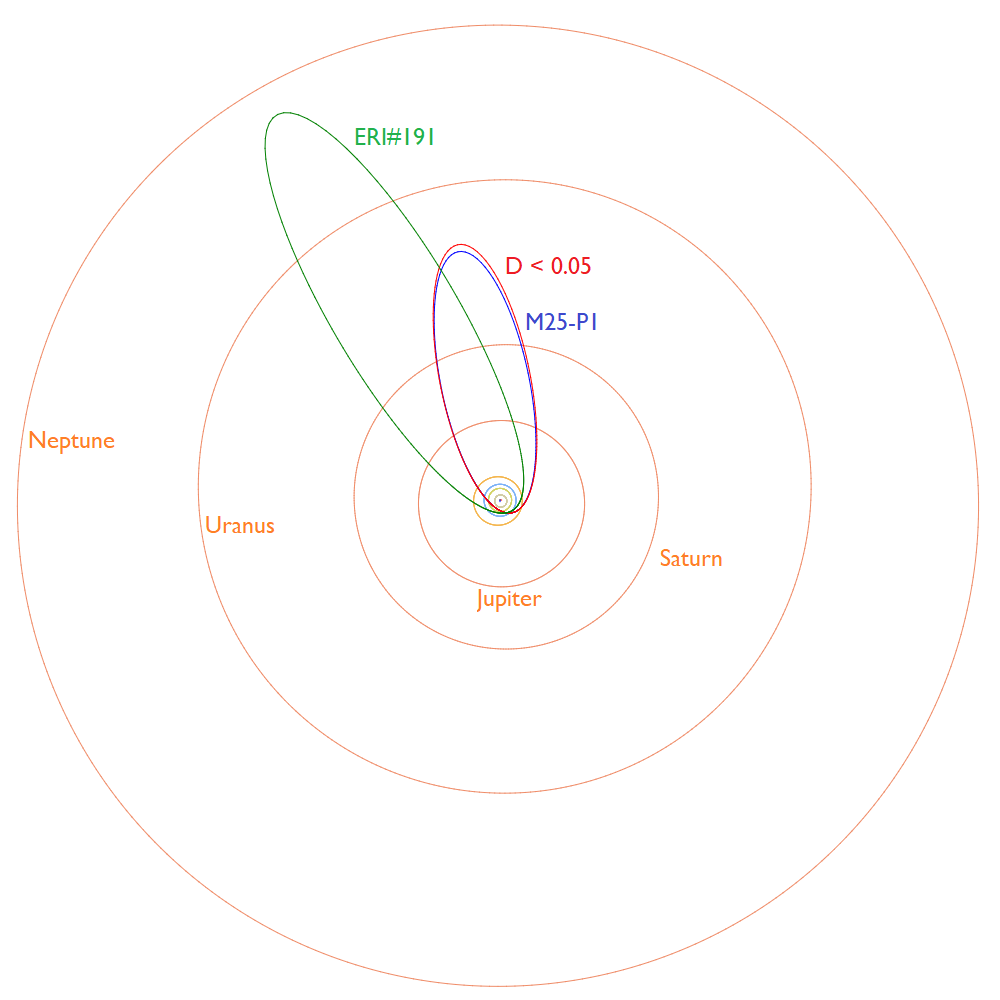
Figure 11 – Comparing the mean orbit based on the shower identification according to the two methods, blue is for M2025-P1 and red for the alternative shower search method with DD < 0.05 in Table 1. (Plotted with the Orbit visualization app provided by Pető Zsolt).
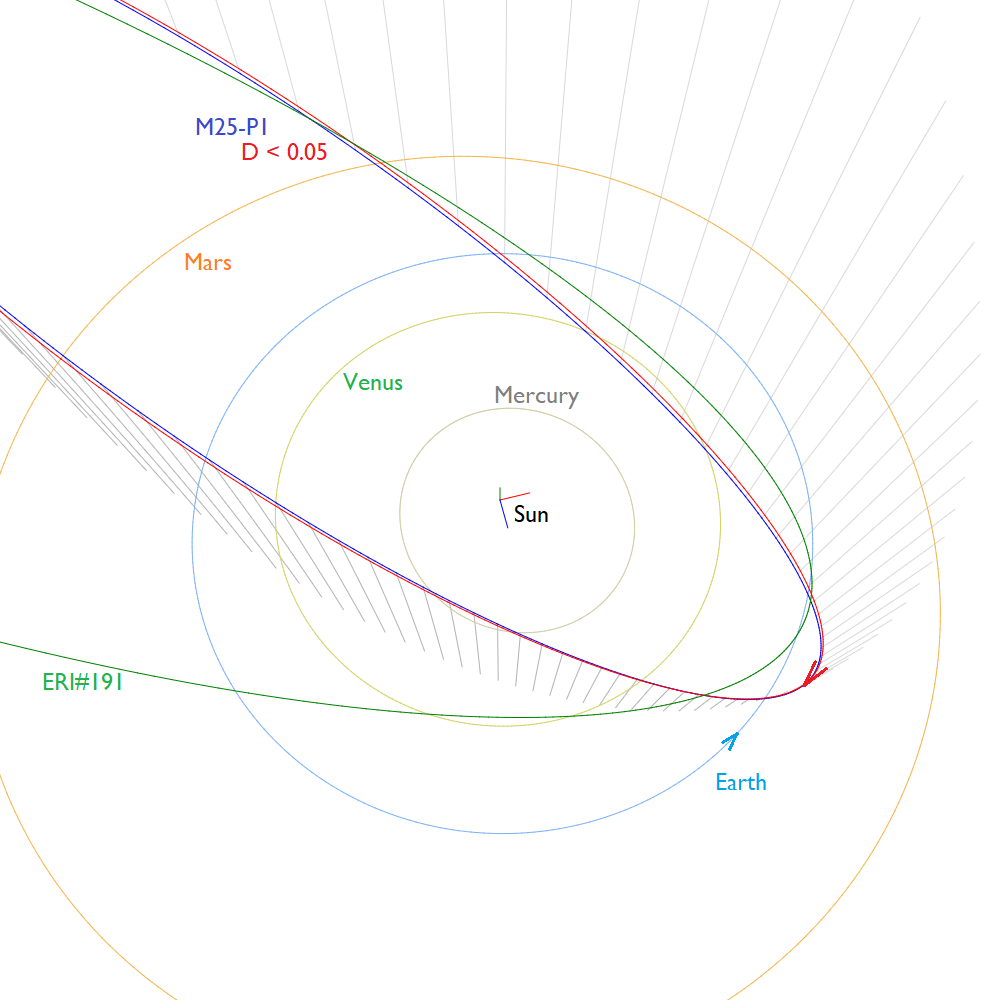
Figure 12 – Comparing the mean orbits in the inner solar system, blue is for M2025-P1 and red for the other shower search method with DD < 0.05 in Table 1. (Plotted with the Orbit visualization app provided by Pető Zsolt).
The Tisserand’s parameter Tj identifies the orbit as of a long-period comet type in this case with a retrograde orbit. A parent-body search top 10 includes candidates with a threshold for the Drummond DD criterion value lower than 0.25 but none of which can be associated with any certainty (Table 2). Comet C/1852 K1 (Chacornac) is considered as a likely source for the eta Eridanids (ERI#191) (Jenniskens, 2024, page 445). It would be up to meteoroid stream modelers to reconstruct the dynamic orbit evolution to see if there could be any connection between this comet and the different meteor showers that could be related.
Table 1 – Comparing the new meteor shower, derived by two different methods, M2025-P1 the orbital parameters as initially derived, the parameters under DD < 0.05 were derived from the method described in Section 3.
| M2025-P1 | DD < 0.05 | |
| λʘ (°) | 125.8 | 126.1 |
| λʘb (°) | 122.7 | 123.6 |
| λʘe (°) | 130.2 | 130.2 |
| αg (°) | 29.8 | 29.8 |
| δg (°) | –20.6 | –20.6 |
| Δαg (°) | +0.79 | +0.67 |
| Δδg (°) | +0.56 | +0.48 |
| vg (km/s) | 61.4 | 61.5 |
| λg (°) | 19.5 | 19.5 |
| λg – λʘ (°) | 253.4 | 253.3 |
| βg (°) | –30.6 | –30.3 |
| a (A.U.) | 12.5 | 13.5 |
| q (A.U.) | 0.8654 | 0.8638 |
| e | 0.9308 | 0.9362 |
| i (°) | 124.2 | 124.6 |
| ω (°) | 45.76 | 46.01 |
| Ω (°) | 306.27 | 306.47 |
| Π (°) | 352.04 | 352.48 |
| Tj | –0.22 | –0.26 |
| N | 32 | 27 |
Table 2 – Top ten matches of a search for possible parent bodies with DD < 0.25.
| Name | DD |
| C/1877 G1 (Winnecke) | 0.111 |
| C/1852 K1 (Chacornac) | 0.121 |
| C/1886 J1 (Brooks) | 0.165 |
| C/2020 H2 (Pruyne) | 0.172 |
| 273P/Pons-Gambart | 0.208 |
| C/2020 A2 (Iwamoto) | 0.215 |
| C/2013 UQ4 (Catalina) | 0.234 |
| C/1994 G1-A (Takamizawa-Levy) | 0.247 |
| C/1994 G1-B (Takamizawa-Levy) | 0.25 |
| C/1925 G1 (Orkisz) | 0.25 |
Activity in past years
A search in older GMN orbit data resulted in one possible orbit with DD < 0.06 in 2020, one in 2021, 16 in 2022, 17 in 2023 and 33 orbits in 2024. SonotaCo Net has 18 orbits with DD < 0.06 in different years from 2007 onwards. EDMOND had only seven orbits with DD < 0.06 between 2008 and 2015 but this network had rather poor coverage of the Southern hemisphere. No other meteor orbit datasets were checked. The activity in the past years indicates that M2025-P1 is an annual shower.
Conclusion
The discovery of a new meteor shower with a radiant in the constellation of Eridanus based on thirty-two meteors during 2025 July 25 – August 3 has been confirmed by using two independent meteor shower search methods. The resulting mean orbits for both search methods are in good agreement. All meteors appeared during the solar-longitude interval 122° – 131°, with most events around 28–29 July (λʘ = 125.6°). Orbits of this meteor shower were detected in previous years, but the presence of the nearby eta Eridanids as a much stronger source is a likely explanation why M2025-P1 hasn’t been detected earlier.
Acknowledgment
This report is based on the data of the Global Meteor Network (Vida et al., 2020a; 2020b; 2021) which is released under the CC BY 4.0 license. We thank all 825 participants in the Global Meteor Network project for their contribution and perseverance. A list with the names of the volunteers who contribute to GMN has been published in the 2024 annual report (Roggemans et al., 2025).
References
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Jenniskens P. (2024). Atlas of Earth’s meteor showers. Elsevier, Cambridge, United states. ISBN 978-0-443-23577-1.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Jopek T. J., Rudawska R. and Pretka-Ziomek H. (2006). “Calculation of the mean orbit of a meteoroid stream”. Monthly Notices of the Royal Astronomical Society, 371, 1367–1372.
Moorhead A. V., Clements T. D., Vida D. (2020). “Realistic gravitational focusing of meteoroid streams”. Monthly Notices of the Royal Astronomical Society, 494, 2982–2994.
Roggemans P., Johannink C. and Campbell-Burns P. (2019a). “October Ursae Majorids (OCU#333)”. eMetN Meteor Journal, 4, 55–64.
Roggemans P., Campbell-Burns P., Kalina M., McIntyre M., Scott J. M., Šegon D., Vida D. (2025). “Global Meteor Network report 2024”. eMetN Meteor Journal, 10, 67–101.
Southworth R. B. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithsonian Contributions to Astrophysics, 7, 261–285.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020a). “Estimating trajectories of meteors: an observational Monte Carlo approach – I. Theory”. Monthly Notices of the Royal Astronomical Society, 491, 2688–2705.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020b). “Estimating trajectories of meteors: an observational Monte Carlo approach – II. Results”. Monthly Notices of the Royal Astronomical Society, 491, 3996–4011.
Vida D., Šegon D., Gural P. S., Brown P. G., McIntyre M. J. M., Dijkema T. J., Pavletić L., Kukić P., Mazur M. J., Eschman P., Roggemans P., Merlak A., Zubrović D. (2021). “The Global Meteor Network – Methodology and first results”. Monthly Notices of the Royal Astronomical Society, 506, 5046–5074.