By Paul Roggemans, Damir Šegon, Denis Vida, James M. Scott, Jeff Wood
Abstract: A case study on the delta-Horologiids (DHO#1146) based on Global Meteor Network orbit data identified 34 possible DHO-orbits in 2025. The radiant position was derived as R.A. = 61.4° and decl.= –40.6° with a geocentric velocity of 42.9 km/s. GMN data confirms the existence of this minor meteor shower.
1 Introduction
While looking for unknown sources of meteor activity sometimes radiants are spotted that are unknown to the GMN meteor shower list. The IAU MDC Meteor Shower List includes many more meteor showers than the GMN list, often poorly documented entries that have been detected in recent years. Before the official procedure to announce the discovery of an unknown meteor shower is made, unidentified radiant concentrations are verified with the IAU MDC list. This procedure was followed for a suspect activity in the constellation of Horologium during the night of 9–10 September, 2025. This meteor shower had been reported in 2023 and registered as the delta-Horologiids (#1146), based on 66 meteors recorded by CAMS and 856 meteors recorded by SAAMER radar (Jenniskens, 2023). Apart from the radiant position, the orbital parameters between the two datasets differ a lot. The IAU-MDC working list of meteor showers contains only the orbit parameters based on CAMS-data. An analysis has been made, based on GMN-data and the solution has been reported to the IAU-MDC.
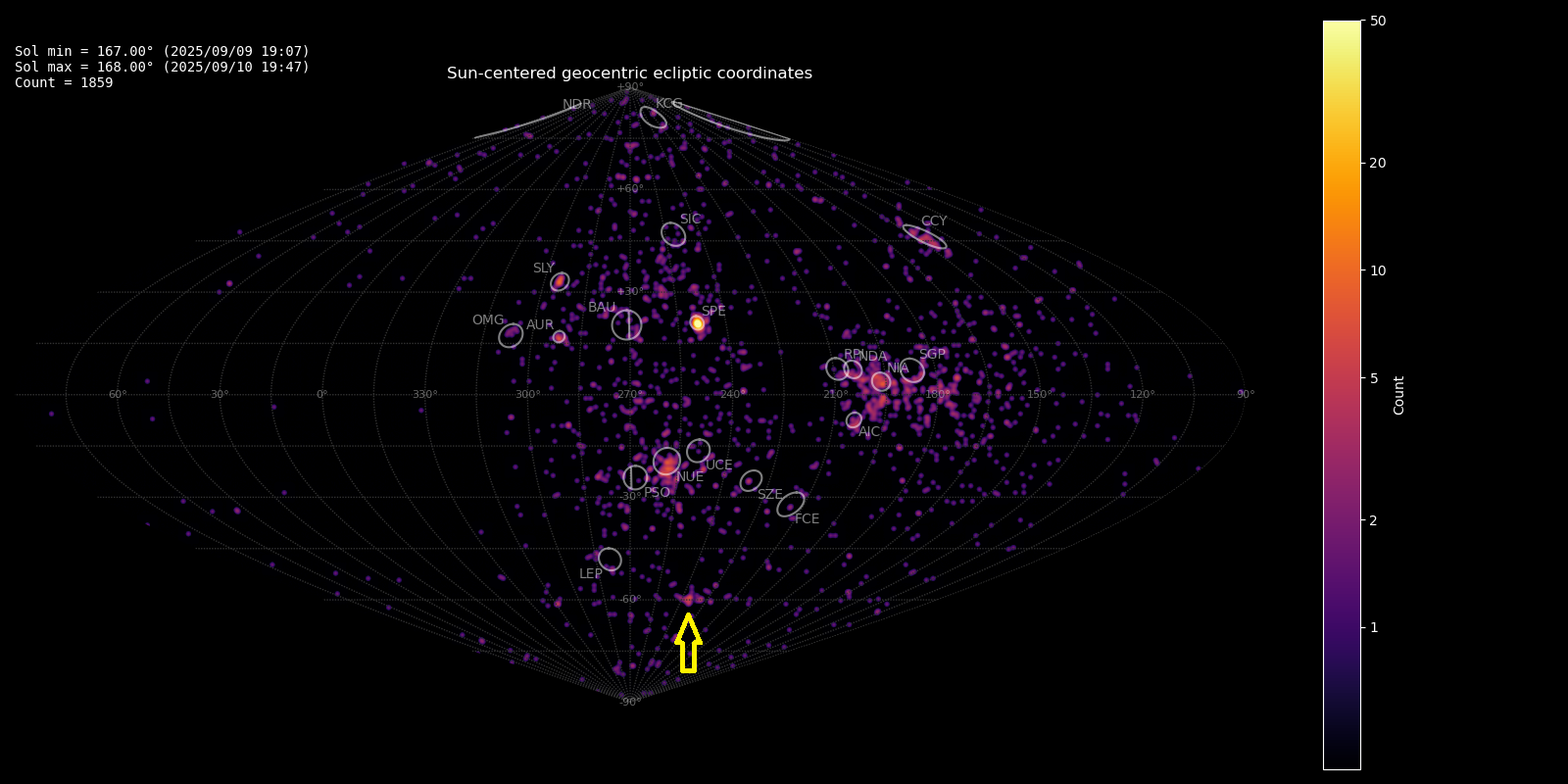
Figure 1 – Heat map with 1859 radiants obtained by the Global Meteor network in 9–10 September, 2025. The position of the delta-Horologiids in Sun-centered geocentric ecliptic coordinates is marked with a yellow arrow.
2 GMN shower identification results
The GMN shower association criterion assumes that meteors within 1° in solar longitude, within an association radius from radiant (2.9° in this case), and within 10% in geocentric velocity of a shower reference location are members of that shower. Further details about the shower association are explained in Moorhead et al. (2020). Using these meteor shower selection criteria, 34 orbits have been associated in 2025 with the delta-Horologiids. The mean orbit has been listed in Table 1.
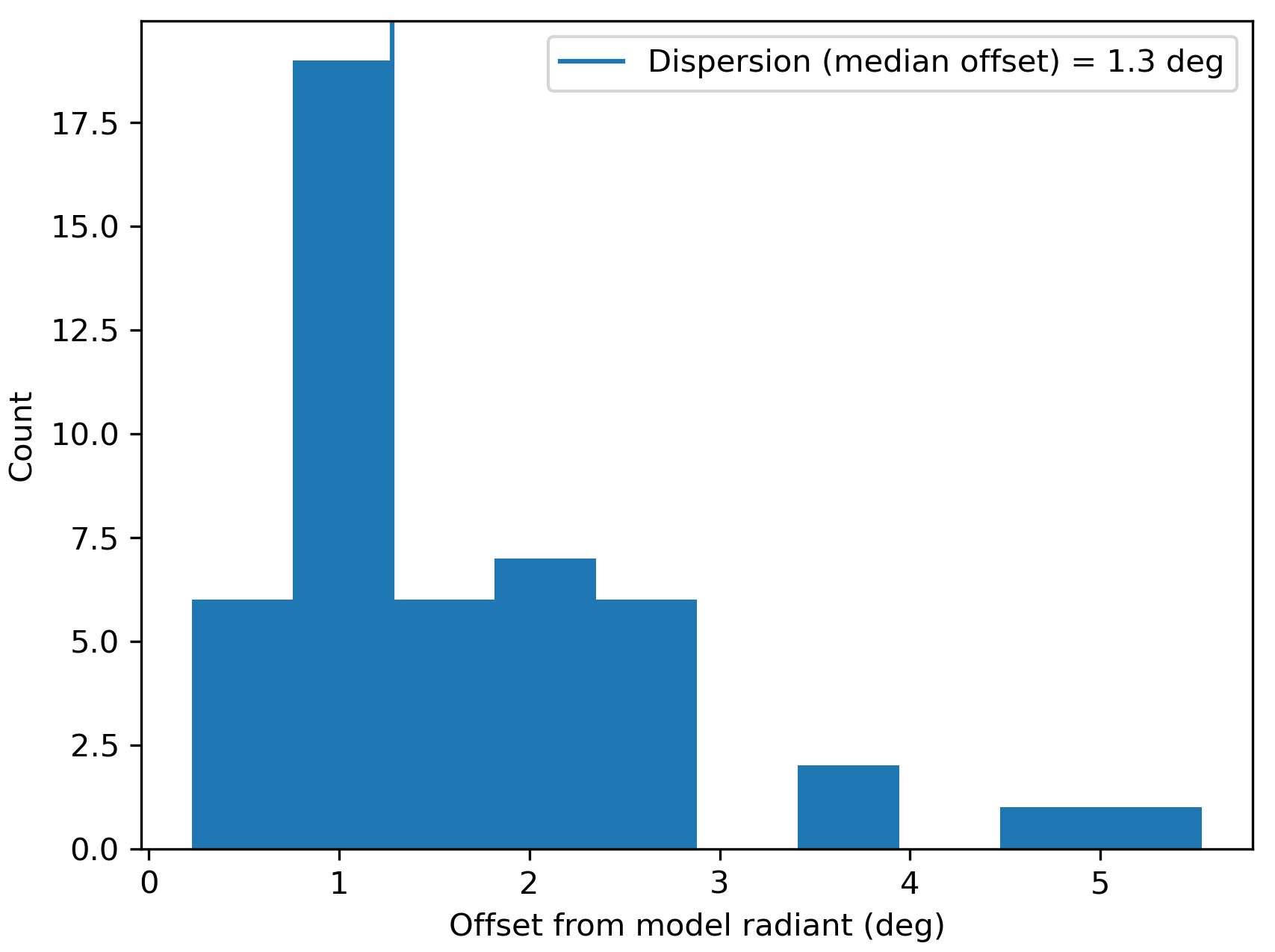
Figure 2 – Dispersion on the radiant position.
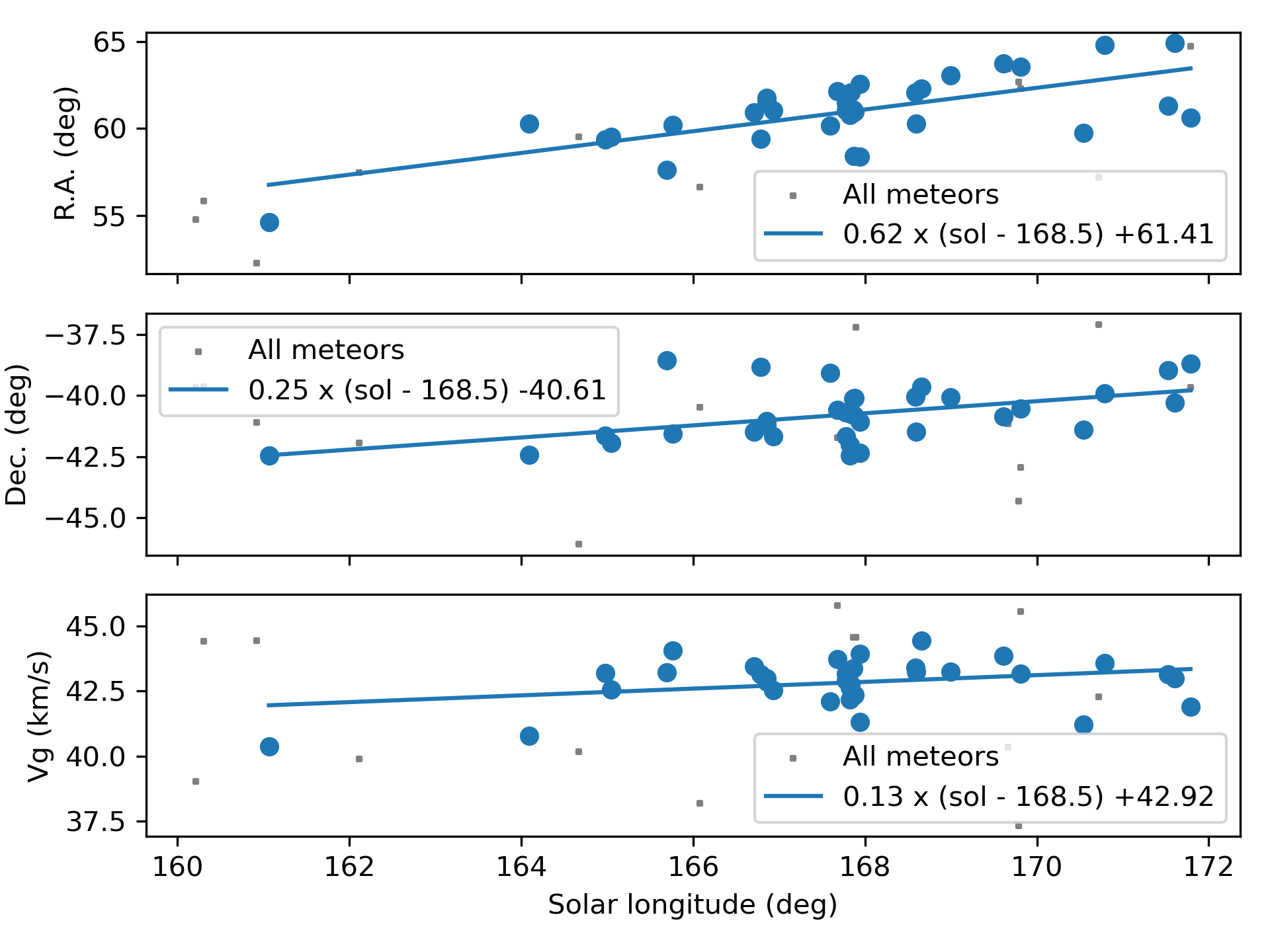
Figure 3 – The radiant drift.
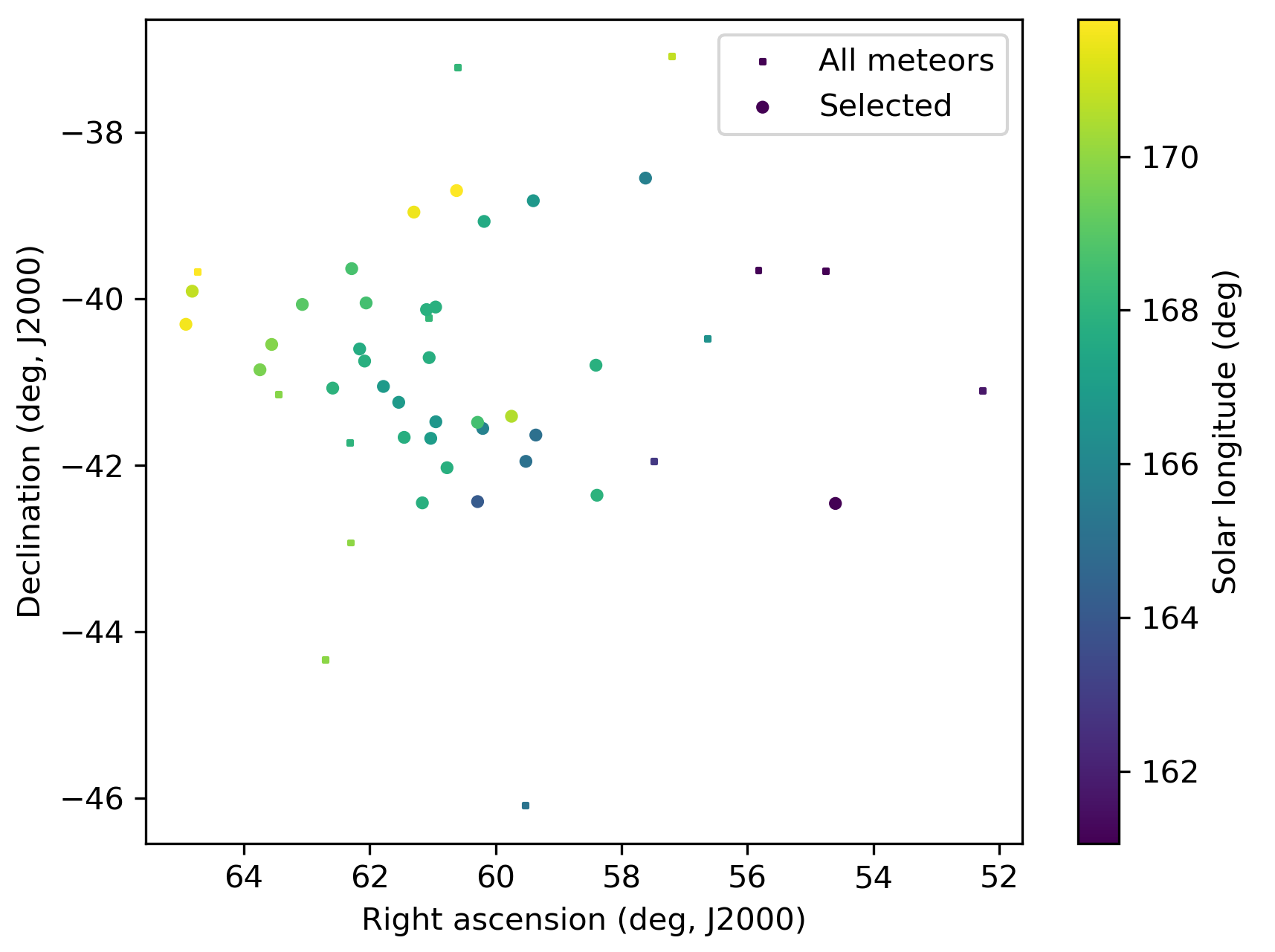
Figure 4 – The radiant distribution during the solar-longitude interval 161.0° – 172.0° in equatorial coordinates.
Figures 5 and 6 clearly show that the shower activity source appeared on top of the sporadic background noise.
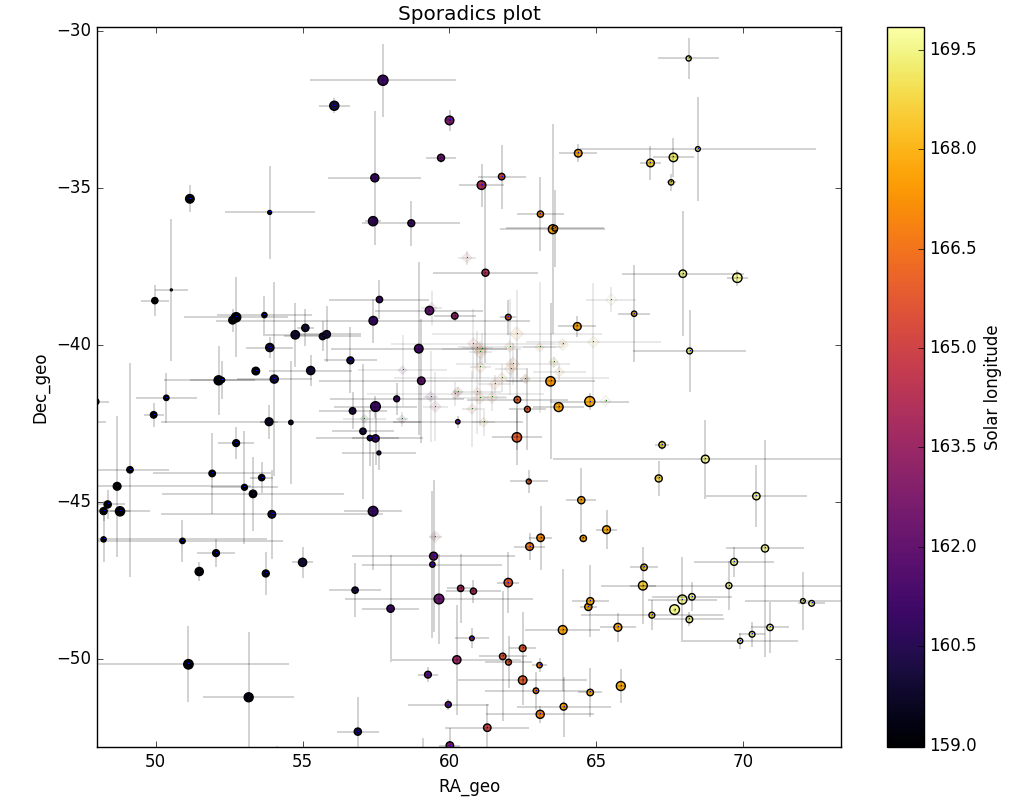
Figure 5 – All non shower meteor radiants in geocentric equatorial coordinates during the shower activity. The pale diamonds represent the new shower radiants plots, error bars represent two sigma values in both coordinates.
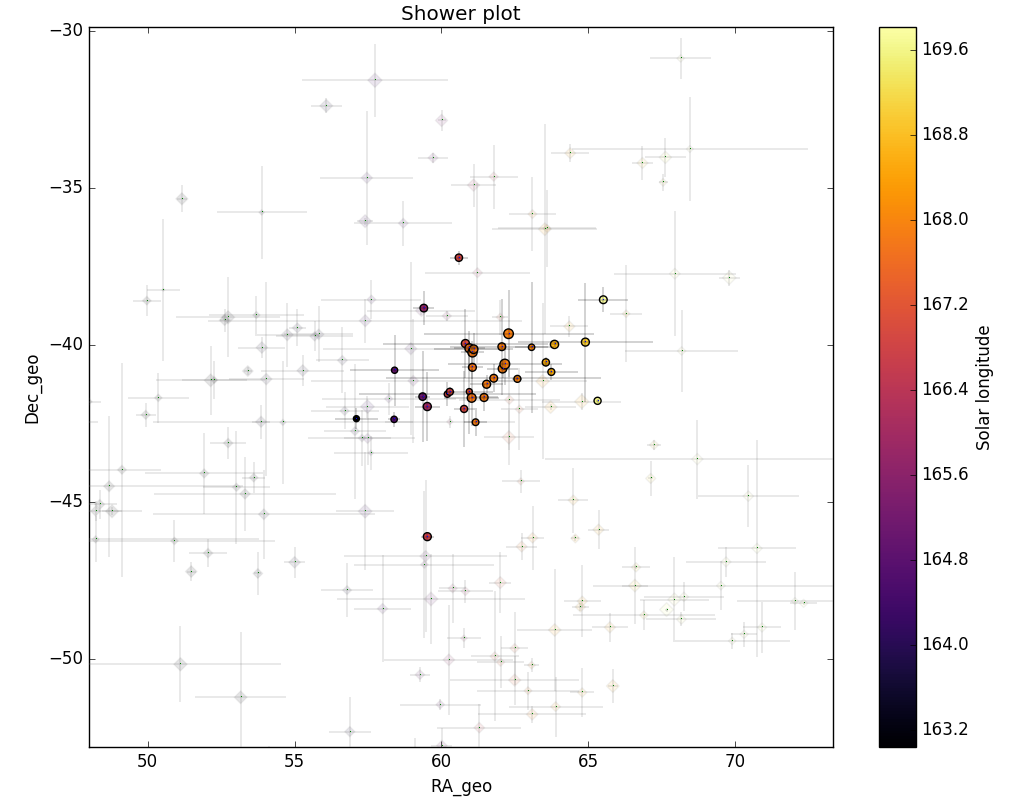
Figure 6 – The reverse of Figure 5, now the shower meteors are shown as circles and the non shower meteors as grayed out diamonds. Note that there are no other groups of meteor radiants to be seen in the vicinity of the possibly new meteor shower.
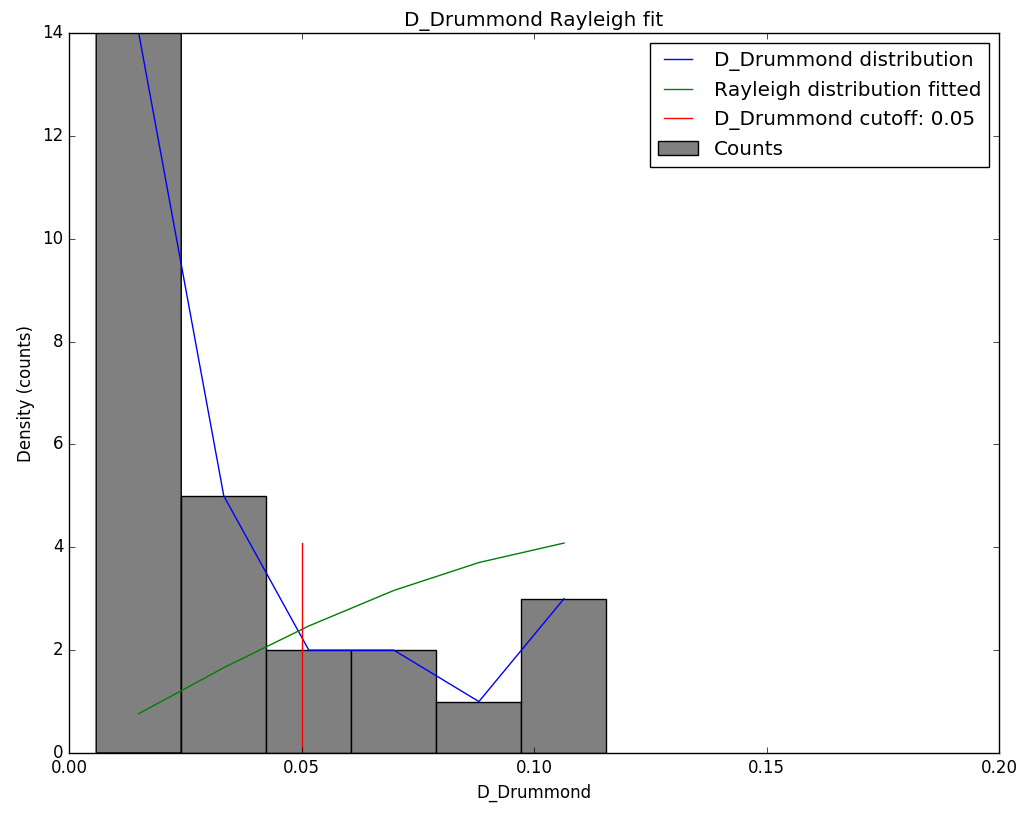
Figure 7 – Rayleigh distribution fit and Drummond DD criterion cutoff.
3 Another search method
Meteor shower identification strongly depends on the methodology used to select candidate shower members. The sporadic background is everywhere present at the sky which risks to contaminate selections of shower candidates. Using a radiant location is a straightforward method to classify shower meteors. In order to double check GMN meteor shower detections another method is used, based on orbit similarity criteria. This approach serves as a second opinion to make sure that no spurious radiant concentrations are mistaken as new meteor showers.
The visible concentration of radiant points was extracted for the time interval of 161° < λʘ < 172°, arbitrarily limited in Sun-centered geocentric ecliptic coordinates with
220° < λ–λʘ < 250° and –48° < β < –69°. This selection includes most of the possible meteor shower members as well as the sporadic sources within this interval. This preselection included 162 meteor orbits, used to compute a first mean orbit for this sample. We didn’t use median values to derive a mean orbit since a vectoral solution like the method of Jopek et al. (2006) is more appropriate for orbital elements with angular values.
This first mean orbit serves as a reference orbit to start an iterative procedure to approach a mean orbit which is the most representative orbit for the similar orbits within the sample, removing outliers and sporadic orbits. This method has been described before (Roggemans et al., 2019). Three different discrimination criteria are combined in order to have only those orbits which fit the different criteria thresholds. The D-criteria that we use are these of Southworth and Hawkins (1963), Drummond (1981) and Jopek (1993) combined. The values are considered in five different classes with different thresholds of similarity:
- Low: DSH < 0.2 & DD < 0.08 & DJ < 0.2;
- Medium Low: DSH < 0.125 & DD < 0.05 & DJ < 0.125;
- Medium high: DSH < 0.1 & DD < 0.04 & DJ < 0.1;
- High: DSH < 0.075 & DD < 0.03 & DJ < 0.075.
- Very high: DSH < 0.05 & DD < 0.02 & DJ < 0.05.
Working with D-criteria requires caution as the validity depends much on the type of orbits. The method works fine for high inclined long period orbits, but is less reliable for low inclination, low eccentricity short period orbits. The D-criteria values are no more than an indication for the degree of similarity between an orbit and a reference orbit.
The Rayleigh distribution fit pointed at a DD value of 0.05 as the orbital similarity threshold value cutoff (Figure 7). This method resulted in a mean orbit with 31 related orbits that fit within the similarity threshold with DSH < 0.125, DD < 0.05 and DJ < 0.125, recorded 2025 September 5 – 14. The plot of the radiant positions in equatorial coordinates, color coded for different D-criteria thresholds, shows a clear concentration in Right Ascension from about 57° to 66° and –38° to –43° in declination (Figure 9), see also Figure 4.
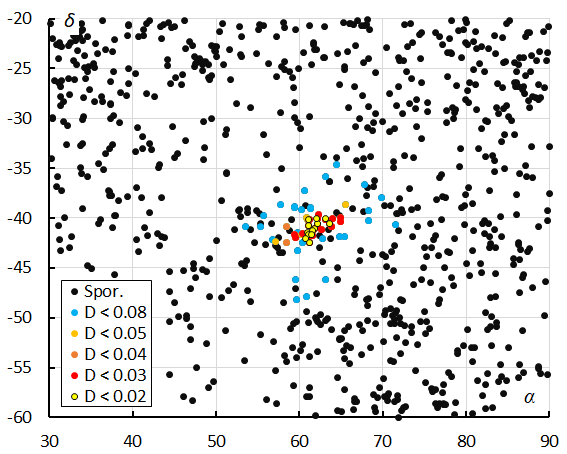
Figure 8 – The radiant distribution during the solar-longitude interval 161° – 172° in equatorial coordinates, color coded for five threshold values of the DD orbit similarity criterion.
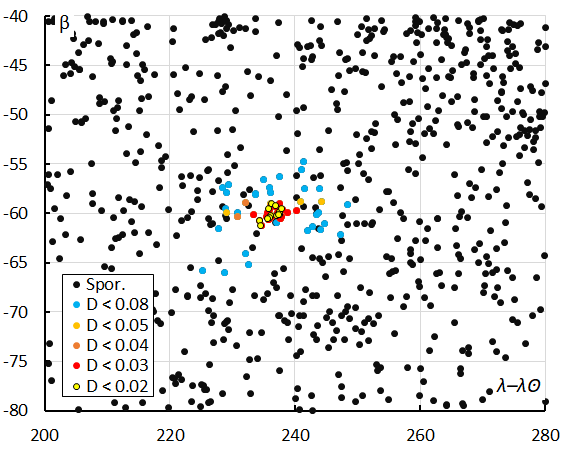
Figure 9 – The radiant distribution during the solar-longitude interval 161° – 172° in Sun-centered geocentric ecliptic coordinates, color coded for five threshold values of the DD orbit similarity criterion.
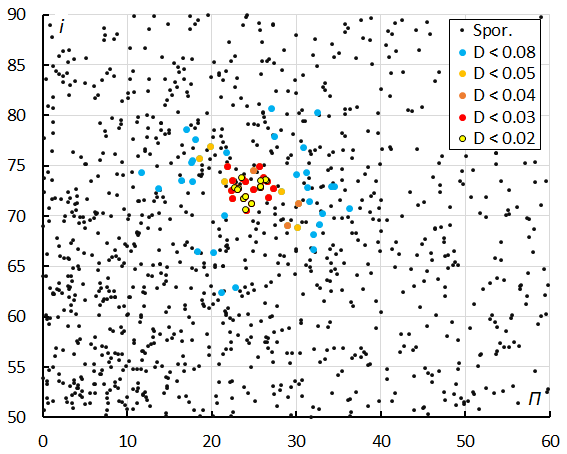
Figure 10 – The diagram of the inclination i versus the longitude of perihelion Π color coded for five classes of D criterion threshold.
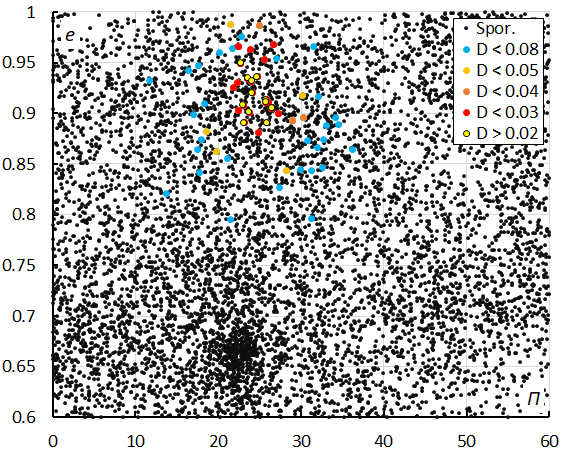
Figure 11 – Diagram of eccentricity e versus the longitude of perihelion Π, color coded for different threshold classes of the orbit similarity criteria.
Figure 10 shows inclination i against the longitude of perihelion Π. The delta-Horologiids appear well concentrated in inclination and in longitude of perihelion. Figure 11 shows that there is more dispersion in eccentricity against longitude of perihelion. The blue dots are associations that fit the threshold class with DSH < 0.2 & DD < 0.08 & DJ < 0.2 and appear to be outliers, indicating that the cutoff value DD < 0.05 obtained from the Rayleigh distribution fit is valid. The concentration below DHO#1146 are the chi-Cygnids (CCY#757) and the newly discovered M2025-S1 meteors. Figure 12 shows the distribution of eccentricity versus inclination.
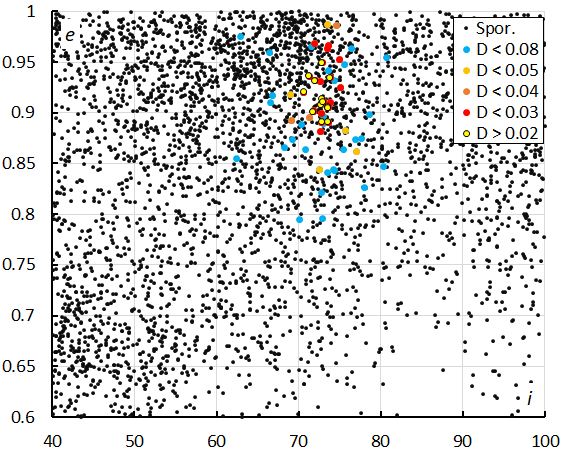
Figure 12 – Diagram of eccentricity e versus inclination i, color coded for different threshold classes of the orbit similarity criteria.
4 Comparing both methods
The first method mainly looks at the radiant positions for the classification. When we apply the D-criteria, 28 of the 34 selected meteors fulfill the threshold values of DSH < 0.125, DD < 0.05 and DJ < 0.125 for the mean orbit obtained by the GMN method, an outlier at λʘ = 161.07° fails completely in the D-criteria. The activity period probably starts after λʘ = 163°.
26 meteors were identified as DHO#1146 by both methods, eight were found by the GMN method but ignored by the D-criteria method. Five were found by the D-criteria method but ignored by the GMN method. Despite the difference between the samples based on the two different methods, the final mean orbits are in very good agreement although the method based on D-criteria thresholds tends to select slightly faster meteors.
5 Orbit and parent body
Figure 13 shows the orbits for the different solutions in the inner solar system. The dust of DHO#1146 crosses the Earth orbit at its ascending node. Meteoroids hit the Earth from deep south of the ecliptic. With an inclination of about 72° the orbital plane of this meteoroid stream is very steep on the ecliptic. The descending node crosses the ecliptic plane relatively close to the orbit of Jupiter.
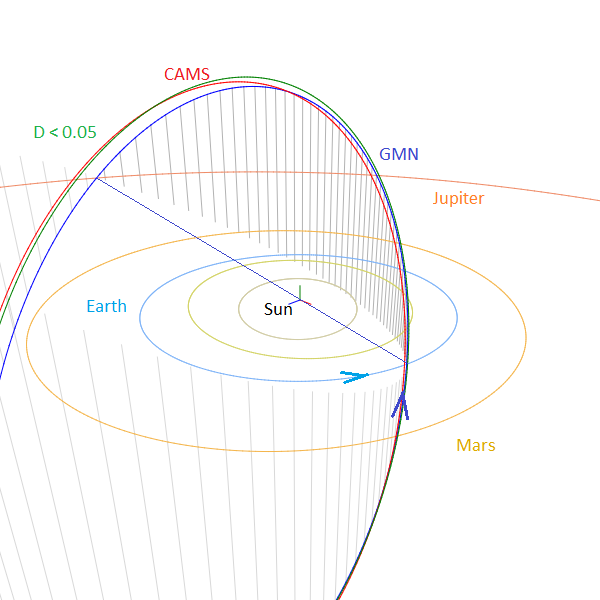
Figure 13 – Comparing the mean orbits for different solutions, blue is based on the GMN method, green for the D-criteria method with DD < 0.05 and red for CAMS data in Table 1, close-up at the inner Solar System. (Plotted with the Orbit visualization app provided by Pető Zsolt).
The Tisserand’s parameter relative to Jupiter, Tj identifies the orbit as of a Mellish-type toroidal shower, because of its high inclination, named after comet C/1917 F1 (Mellish) which was the first numbered of this type. A parent-body search top 10 includes candidates with a threshold for the Drummond DD criterion value lower than 0.26
(Table 2). It would be up to meteoroid stream modelers to reconstruct the dynamic orbit evolution to see if any of these objects might be dynamically related to this shower. The ablation height in the atmosphere is relatively high and indicate fragile cometary material.
The orbital parameters obtained by GMN in 2025 agree fairly well with the solution published for CAMS by Peter Jenniskens (2023). The orbital parameters derived from SAAMER radar data do not correspond, either these refer to another dust population or reflect some instrumental bias.
Table 1 – Comparing CAMS to GMN 2025 solutions derived by two different methods, the parameters under DD < 0.05 were derived from the method described in Section 3.
| GMN 2025 | DD < 0.05 | CAMS | |
| λʘ (°) | 168.5 | 167.9 | 168.5 |
| λʘb (°) | 160.0 | 163.0 | 163 |
| λʘe (°) | 175.0 | 171.6 | 173 |
| αg (°) | 61.4 | 61.2 | 60.8 |
| δg (°) | –40.6 | –40.8 | –40.0 |
| Δαg (°) | +0.62 | +0.59 | +0.10 |
| Δδg (°) | +0.25 | +0.13 | +0.77 |
| vg (km/s) | 42.9 | 43.2 | 43.6 |
| Hb (km) | 106.3 | 106.6 | 108.0 |
| He (km) | 93.1 | 93.0 | 92.0 |
| Hp (km) | 100.1 | 100.8 | 100.3 |
| MagAp | –0.1 | –0.4 | – |
| λg (°) | 44.15 | 43.9 | 43.76 |
| λg – λʘ (°) | 235.65 | 236.2 | 235.26 |
| βg (°) | –59.56 | –59.9 | –58.8 |
| a (A.U.) | 8.782 | 11.3 | 13.6 |
| q (A.U.) | 0.902 | 0.910 | 0.907 |
| e | 0.897 | 0.919 | 0.935 |
| i (°) | 72.4 | 72.7 | 74.1 |
| ω (°) | 38.3 | 36.8 | 37.4 |
| Ω (°) | 347.8 | 348.0 | 348.5 |
| Π (°) | 26.2 | 24.8 | 25.2 |
| Tj | 0.94 | 0.81 | 0.71 |
| N | 34 | 31 | 66 |
Table 2 – Top ten matches of a search for possible parent bodies with DD < 0.26.
| Name | DD |
| C/1932 P1 (Peltier-Whipple) | 0.083 |
| 35P/Herschel-Rigollet | 0.136 |
| 2010 QE2 | 0.147 |
| 2022 KL8 | 0.226 |
| C/1900 O1 (Borrelly-Brooks) | 0.227 |
| C/1984 V1 (Levy-Rudenko) | 0.228 |
| 161P/Hartley-IRAS | 0.236 |
| 2018 ND1 | 0.244 |
| C/390 Q1 | 0.253 |
| C/1982 M1 (Austin) | 0.258 |
6 Past years activity
In 2024 Global Meteor Network detected 40 DHO#1146 meteors with DSH < 0.125, DD < 0.05 and DJ < 0.125, eleven were detected in 2023, four in 2022 and nothing in the years before. These numbers say more about the Global Meteor Network expansion at the Southern Hemisphere than about the shower activity since the number of cameras increased a lot since 2021. No other camera network data is publicly available to check this Southern Hemisphere activity.
A search through older visual observations shows it has been detected in the past by visual observers. Cuno Hoffmeister was the first who had at least four radiants possibly related to this activity when he was in Namibia in 1937–1938. Dedicated meteor observers such as R. MacIntosh (1926–1935) and J. Morgan (1972–1981) in New Zealand didn’t notice any activity, most likely because both did very little observing from mid-August to late September.
In Australia, Shinkfield from Adelaide observed this activity on one occasion on the night of 8 September 1948 (λʘ = 166°) with a radiant at RA 61° and Dec –40°, mentioning in a letter that there was a burst of activity reaching 5 per hour that night. Maurice Clark’s group recorded them in 1979 when one of his observers, Andrew Pearce, recorded a radiant from RA 60° and Dec. –45° in the predawn hours of 9 September (λʘ = 166°) and again on 12 September (λʘ = 169°) with a radiant at RA 64° and Dec. –43°.
WAMS/NAPOMS observers detected them as delta-Horologiids on several occasions from 1979 to 1998. In summary meteors were recorded from around 2 September through to 17 September with what appears to be a maximum ZHR being between 2 and 4 per hour. The mean radiant position at maximum was RA 62° and Dec. –44°.
7 Conclusion
Global Meteor network observations confirm the existence of the minor meteor shower known as the delta-Horologiids and first reported by Peter Jenniskens based on CAMS low-light video cameras. Visual observers noticed weak activity from this source in the past.
The solution derived from GMN data for 2025 is in good agreement with the result published for CAMS-data, but differs a lot from orbit parameters based on SAAMER radar data as published in Jenniskens (2023)..
Acknowledgment
This report is based on the data of the Global Meteor Network (Vida et al., 2020a; 2020b; 2021) which is released under the CC BY 4.0 license. We thank all 825 participants in the Global Meteor Network project for their contribution and perseverance. A list with the names of the volunteers who contribute to GMN has been published in the 2024 annual report (Roggemans et al., 2025).
References
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Jenniskens P. (2023). Atlas of Earth’s meteor showers. Elsevier, Cambridge, United states. ISBN 978-0-443-23577-1. Page 199.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Jopek T. J., Rudawska R. and Pretka-Ziomek H. (2006). “Calculation of the mean orbit of a meteoroid stream”. Monthly Notices of the Royal Astronomical Society, 371, 1367–1372.
Moorhead A. V., Clements T. D., Vida D. (2020). “Realistic gravitational focusing of meteoroid streams”. Monthly Notices of the Royal Astronomical Society, 494, 2982–2994.
Roggemans P., Johannink C. and Campbell-Burns P. (2019a). “October Ursae Majorids (OCU#333)”. eMetN Meteor Journal, 4, 55–64.
Roggemans P., Campbell-Burns P., Kalina M., McIntyre M., Scott J. M., Šegon D., Vida D. (2025). “Global Meteor Network report 2024”. eMetN Meteor Journal, 10, 67–101.
Southworth R. B. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithsonian Contributions to Astrophysics, 7, 261–285.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020a). “Estimating trajectories of meteors: an observational Monte Carlo approach – I. Theory”. Monthly Notices of the Royal Astronomical Society, 491, 2688–2705.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020b). “Estimating trajectories of meteors: an observational Monte Carlo approach – II. Results”. Monthly Notices of the Royal Astronomical Society, 491, 3996–4011.
Vida D., Šegon D., Gural P. S., Brown P. G., McIntyre M. J. M., Dijkema T. J., Pavletić L., Kukić P., Mazur M. J., Eschman P., Roggemans P., Merlak A., Zubrović D. (2021). “The Global Meteor Network – Methodology and first results”. Monthly Notices of the Royal Astronomical Society, 506, 5046–5074.