By Damir Šegon, Denis Vida and Paul Roggemans
Abstract: A new meteor shower on a Jupiter-family comet orbit (TJ = 2.9 ± 0.1) orbit has been detected during March 18–22, 2025 by the Global Meteor Network. Meteors belonging to the new shower were observed between 357° < λʘ < 3° from a radiant at R.A. = 122° and Decl.= –37° in the constellation of Puppis, with a geocentric velocity of 15.1 km/s. The new meteor shower has been listed in the Working List of Meteor Showers under the temporary name-designation: M2025-F1.
Introduction
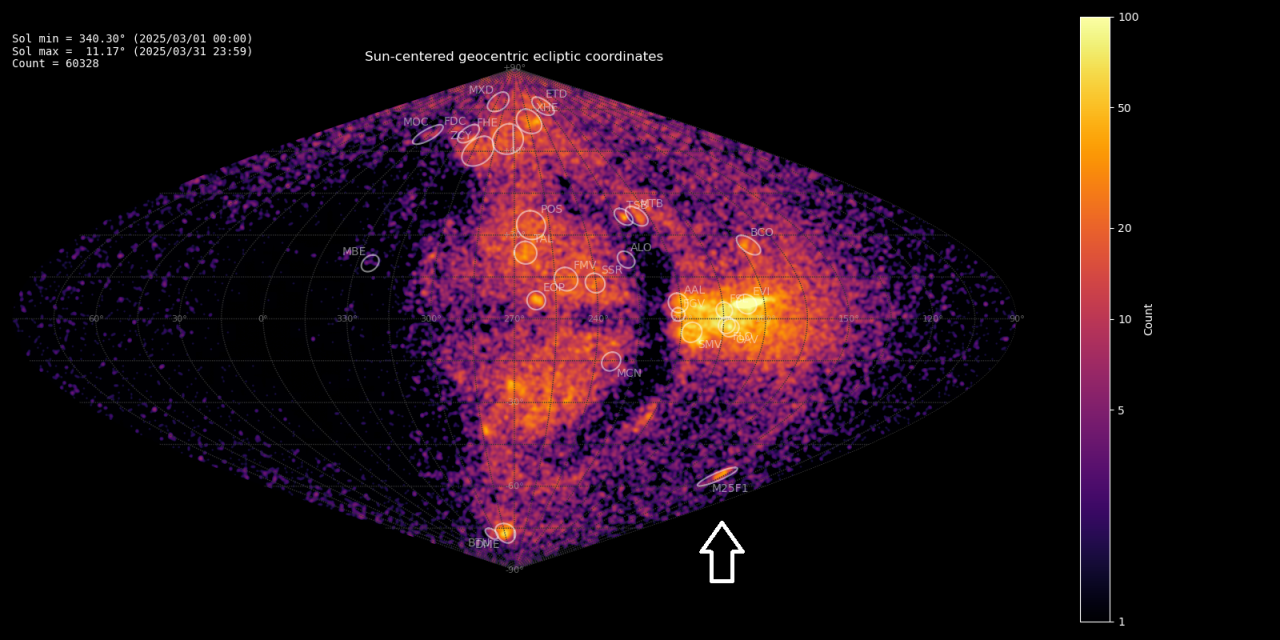
The GMN radiant map for March 2025 shows a trail of related radiants in the constellation of Puppis, with very weak activity that started as early as two weeks before the reported activity period (Figure 1). 150 meteors of this meteor shower were observed by the Global Meteor Network low-light video cameras on 2025 March 18 – 22. The shower was independently observed by cameras in 14 countries across the globe (Australia, Belgium, Bulgaria, Brazil, Canada, Germany, France, Hungary, South Korea, the Netherlands, New Zealand, United Kingdom, United States and South Africa).
The shower had a median geocentric radiant with coordinates R.A. = 121.9°, Decl. = –37.2°, within a circle with a standard deviation of ±1.3° (equinox J2000.0) see Figure 2. The radiant drift in R.A. is –0.35 deg on the sky per degree of solar longitude and –0.81 in Dec., both reference to λʘ = 359.0° (Figures 3 and 4). The median Sun-centered ecliptic coordinates were λ – λʘ = 137.00°, β = –55.49° (Figure 5). The geocentric velocity was very low at 15.1 ± 0.2 km/s.
All meteors appeared during the solar-longitude interval 358.0° – 2.7°, with no clear peak but a plateau lasting roughly between 359.5° – 2.0°.
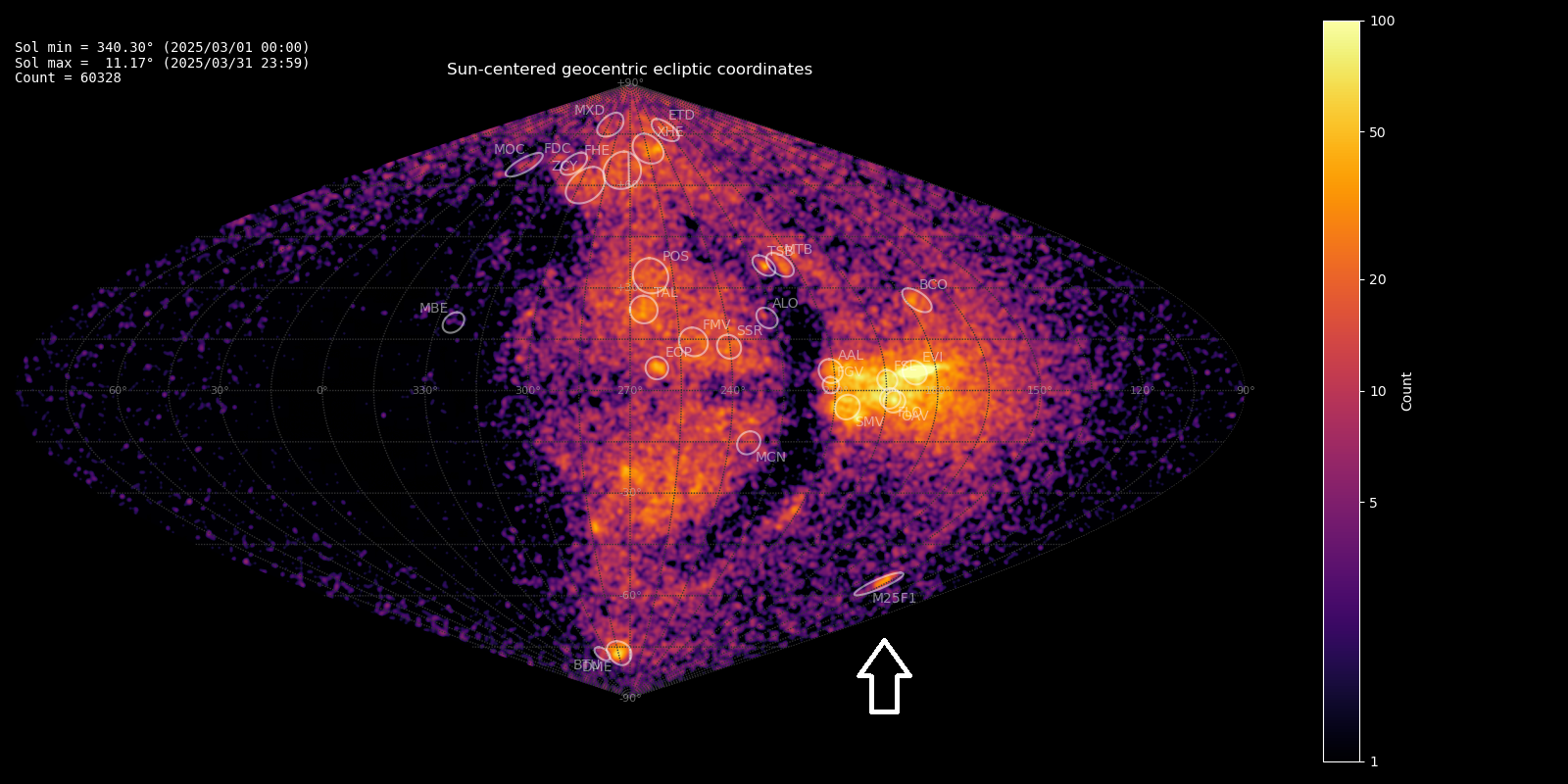
Figure 1 – Heat map with 60328 radiants obtained by the Global Meteor network in March 2025. An extended concentration is visible in Sun-centered geocentric ecliptic coordinates which was identified as a new meteor shower with the temporary identification M2025-F1.
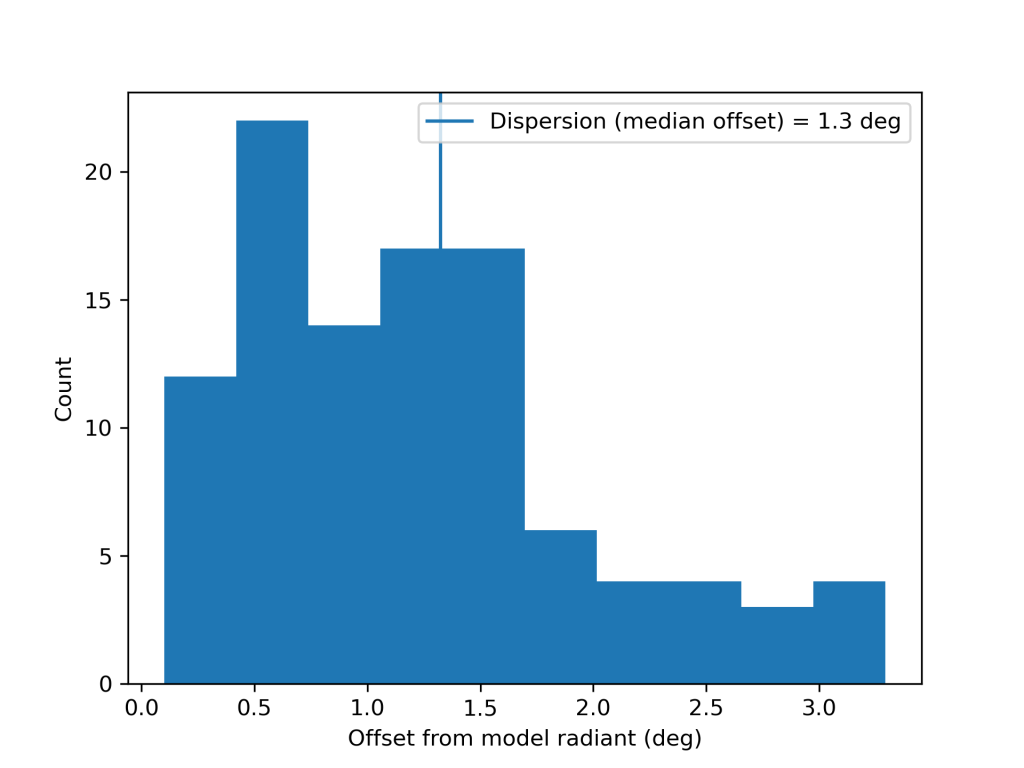
Figure 2 – Dispersion on the radiant position.
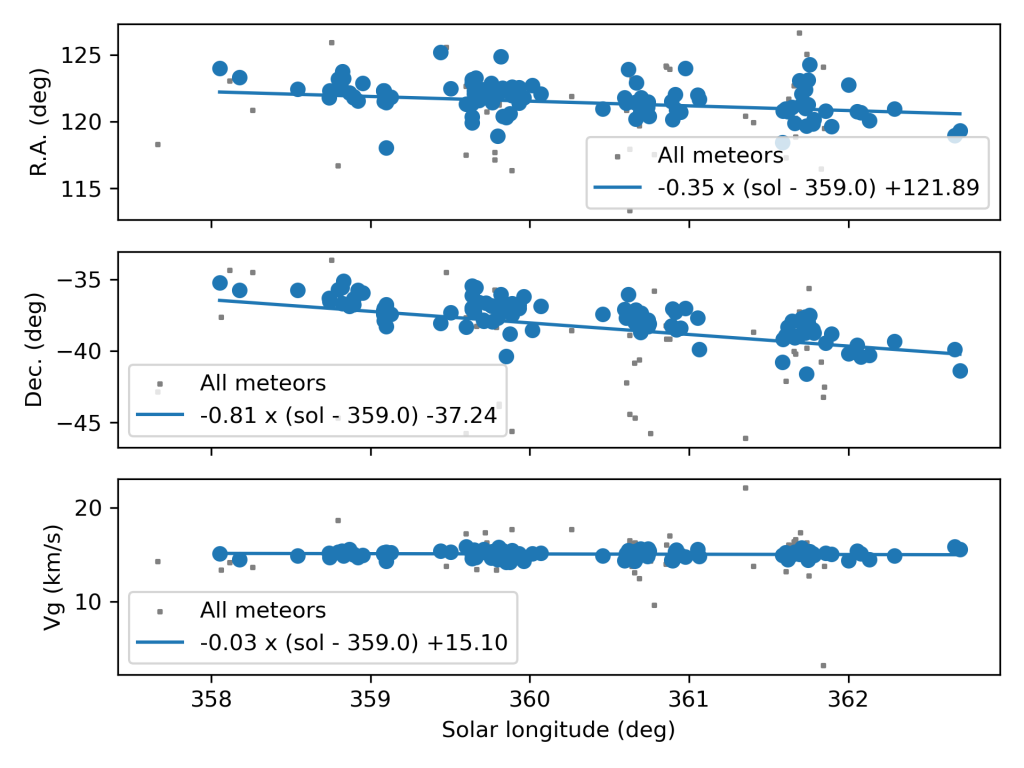
Figure 3 – The radiant drift.
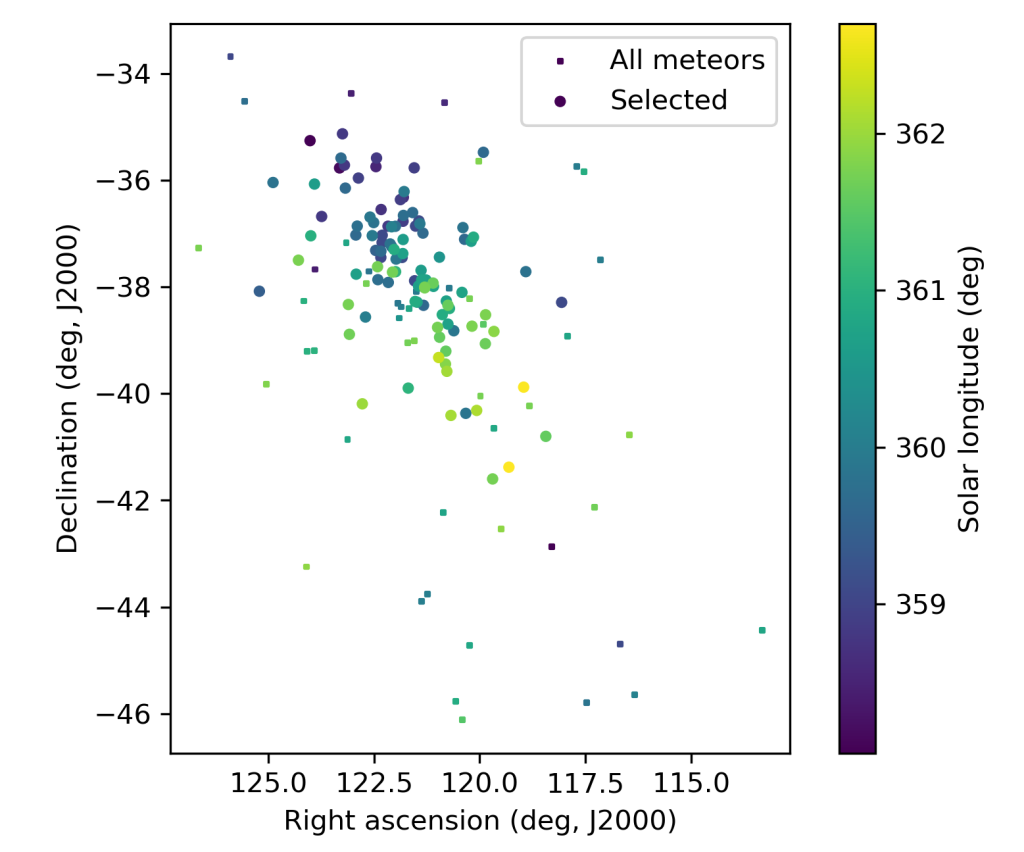
Figure 4 – The radiant distribution during the solar-longitude interval 358.0° – 2.7° in equatorial coordinates.
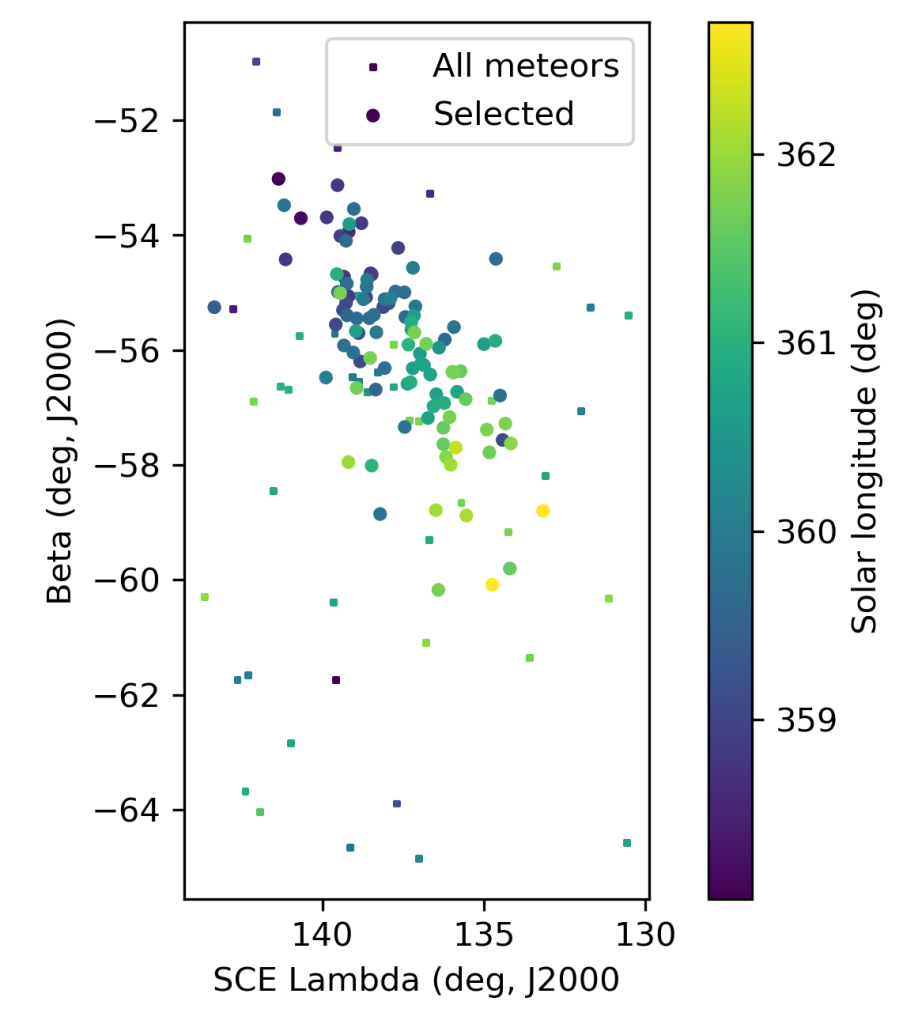
Figure 5 – The radiant distribution during the solar-longitude interval 358.0° – 2.7° in geocentric ecliptical coordinates.
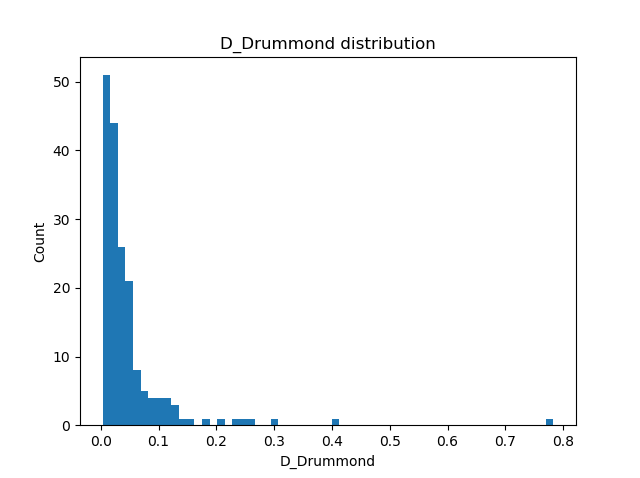
Figure 6 – Histogram of the distribution of the Drummond DD criterion values valid for the final mean orbit.
Discovery and first analysis
We used the procedure as described for some recent cases of possibly new showers in Bootes and Draco (Šegon et al., 2023). The Drummond dissimilarity criteria DD has been chosen for the analysis of the new radiant concentration. A first iteration revealed a clear concentration of orbits, as it can be seen on Figure 6. The Railey distribution fit pointed at a DD value of 0.05 as the orbital similarity cutoff (Figure 7), which resulted in 150 orbits representing the possibly new meteor shower.
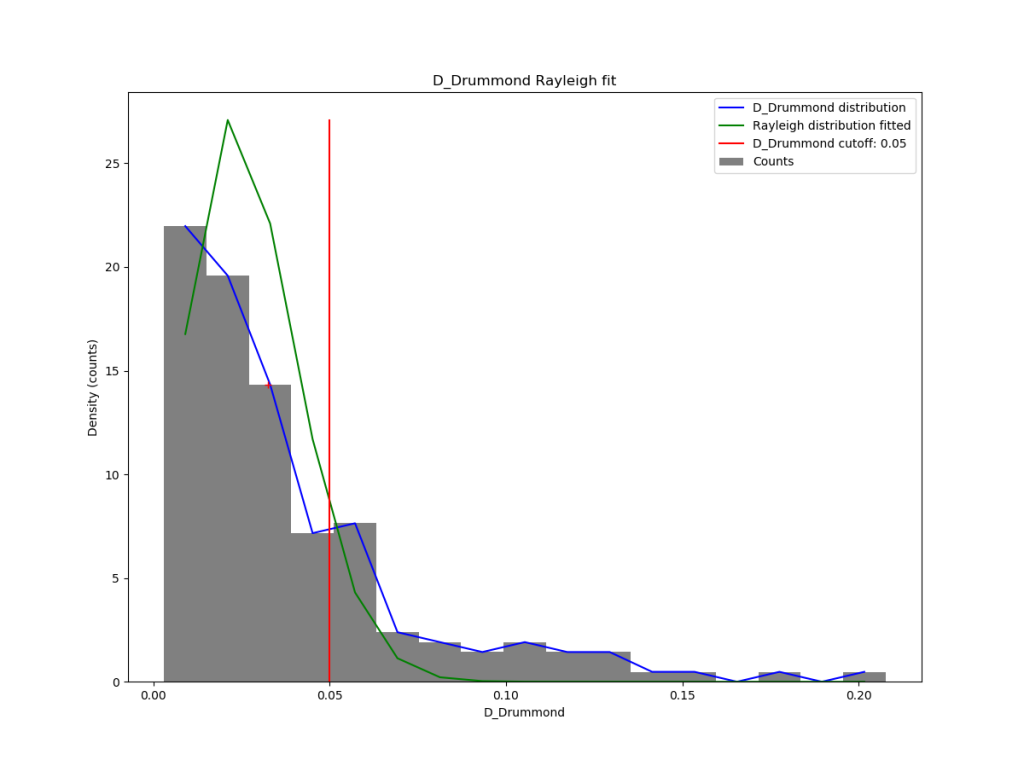
Figure 7 – Rayleigh distribution fit and Drummond DD criterion cutoff.
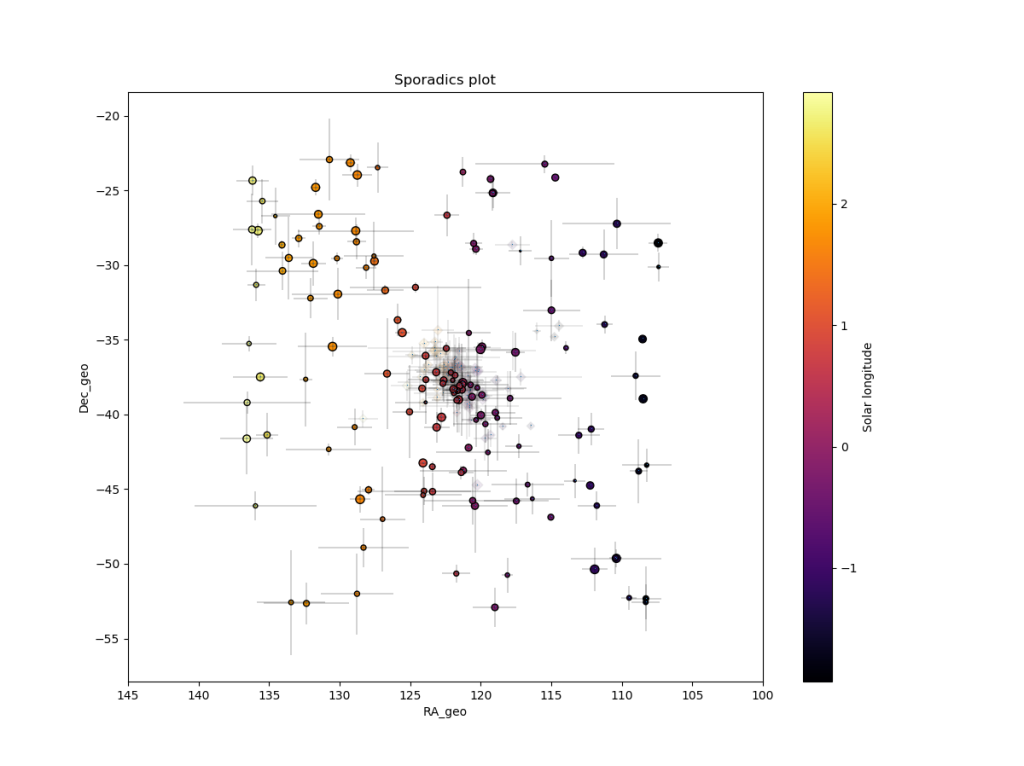
Figure 8 – All non shower meteor radiants in geocentric equatorial coordinates during the shower activity. The pale diamonds represent the new shower radiants plots, error bars represent two sigma values in both coordinates.
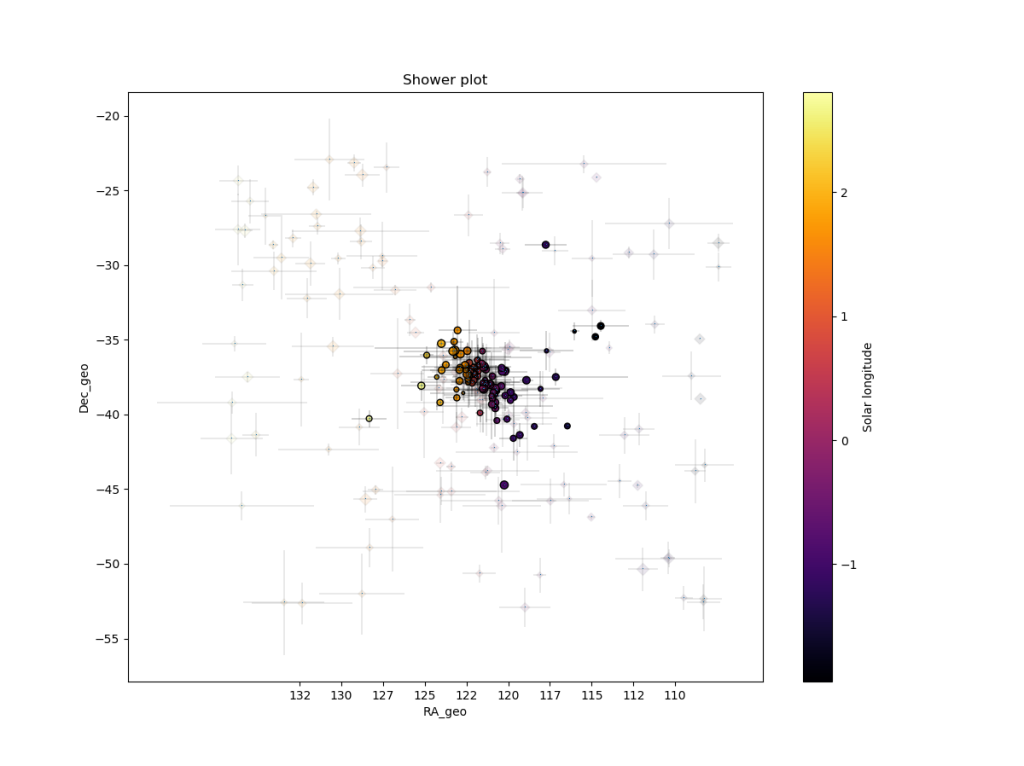
Figure 9 – The reverse of Figure 8, now the shower meteors are shown as circles and the non shower meteors as grayed out diamonds. Note that there are no other groups of meteor radiants to be seen in the vicinity of the possibly new meteor shower.
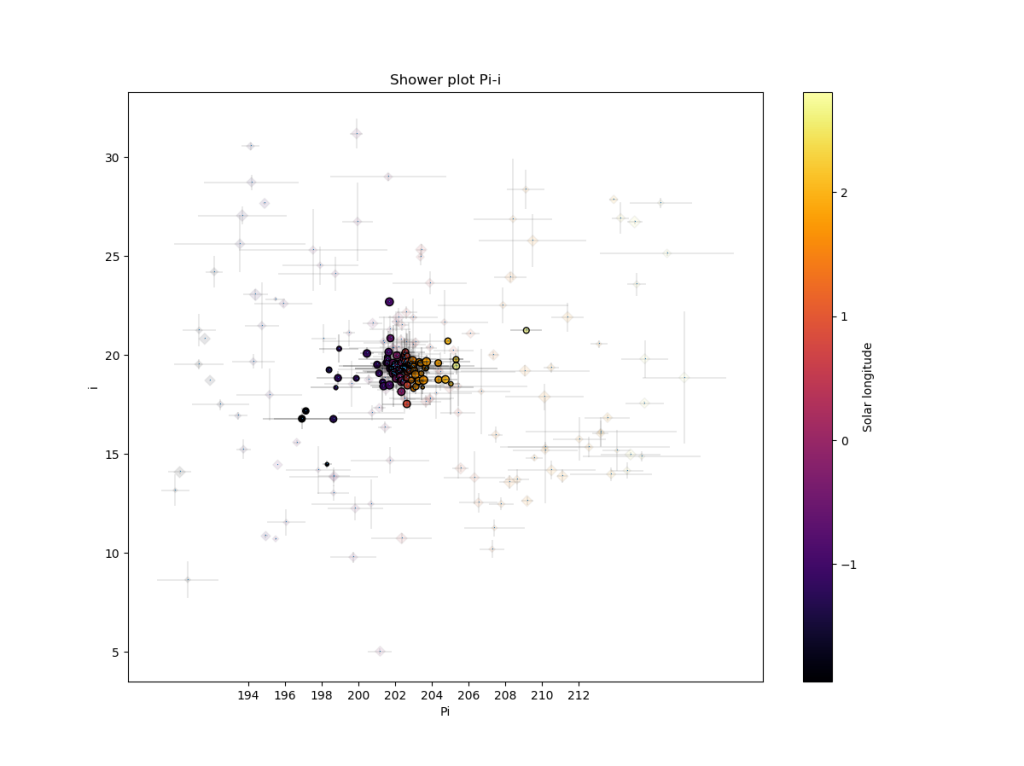
Figure 10 – The diagram of the inclination i against longitude of perihelion Π shows a distinct group of radiants without any other groups to be seen.
The presence of non-shower radiants in the area around the possibly new shower (Figure 8) shows the cutoff to be reliable since the density of meteor radiants does not look affected after removing shower members (plotted as pale diamonds). The plot of the shower meteor radiants in equatorial coordinates shows a very compact group, with a standard deviation of the distances from the average radiant position of about 1.3° (see Figure 9). The Π–i diagram shows a compact group of radiants too (Figure 10), without any other groups of radiants to be seen.
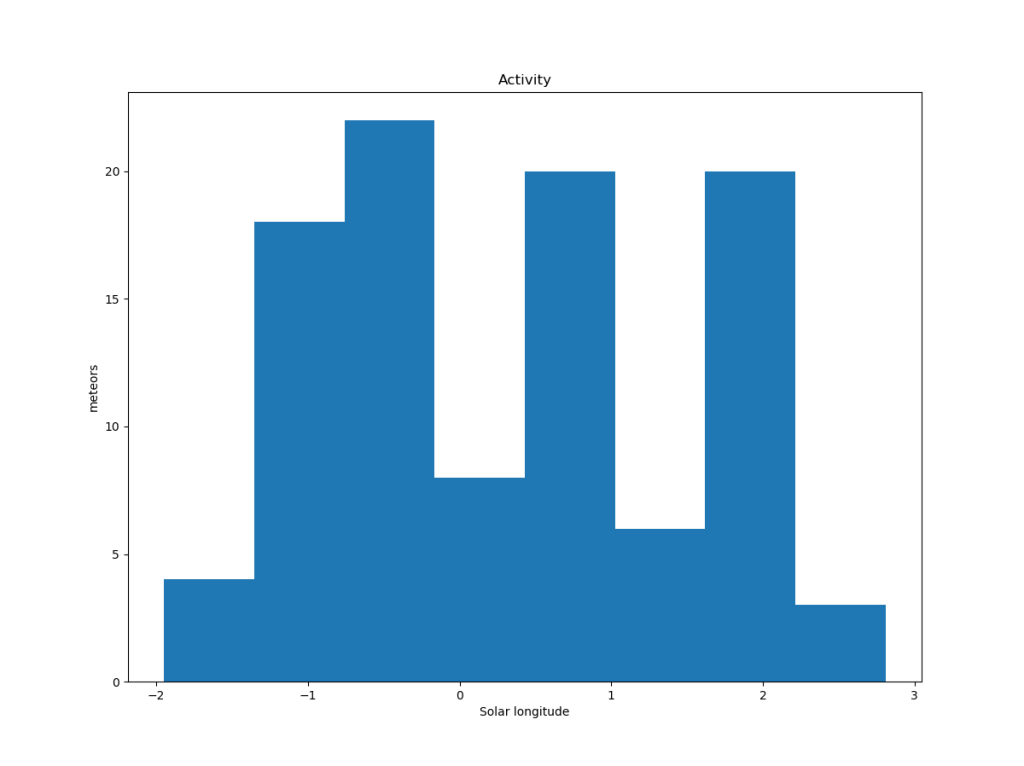
Figure 11 – The activity period with the number of orbits identified as new shower members.
The activity profile (Figure 11) considered in the first analysis shows no clear peak but a plateau 359.5° < λʘ < 2.0° (2025, March 20–22) but it was noticed that more related events could have been detected outside this observing window.
Another search method
Another method has been applied to check this new meteor shower discovery. The starting point here can be any visually spotted concentration of radiant points or any other indication for the occurrence of similar orbits. The method has been described before (Roggemans et al., 2019). The main difference with the method applied in Section 2 is that three different discrimination criteria are combined in order to have only those orbits which fit different criteria. The D-criteria that we use are these of Southworth and Hawkins (1963), Drummond (1981) and Jopek (1993) combined. Instead of using a cutoff value for the D-criteria these values are considered in different classes with different thresholds of similarity. Depending on the dispersion and the type of orbits, the most appropriate threshold of similarity is selected to locate the best fitting mean orbit as the result of an iterative procedure.
To avoid contamination with sporadics the search interval was limited to 357.0° < λʘ < 3.0°. The Global Meteor Network had 14617 meteor orbits in this interval. After some iterations the procedure converged on a mean orbit computed following the method of Jopek et al. (2006) with 132 orbits that fit the D-criteria with DD < 0.05. The resulting mean orbit is in perfect agreement with the initial result. The orbits are compared in Table 1 and for completeness we mention also the mean orbit obtained from the orbits that fit within DD < 0.02.
Table 1 – Comparing the new meteor shower, derived by two different methods, M2025-F1 the orbital parameters as initially derived, DD < 0.05 and DD < 0.02, derived from the method described in Section 3.
| M2025-F1 | DD < 0.05 | DD < 0.02 | |
| λʘ (°) | 359.0 | 0.3 | 359.9 |
| λʘb (°) | 357.5 | 357.1 | 357.3 |
| λʘe (°) | 3.0 | 2.9 | 2.7 |
| αg (°) | 121.9 | 121.7 | 121.7 |
| δg (°) | –37.2 | –37.5 | –37.4 |
| Δαg (°) | –0.35 | – | – |
| Δδg (°) | –0.81 | – | – |
| vg (km/s) | 15.1 | 15.2 | 15.1 |
| λg (°) | 137.93 | 137.9 | 137.9 |
| λg – λʘ (°) | 138.93 | 137.7 | 138.0 |
| βg (°) | –55.46 | –55.7 | –55.7 |
| a (A.U.) | 2.71 | 2.75 | 2.76 |
| q (A.U.) | 0.967 | 0.966 | 0.967 |
| e | 0.643 | 0.649 | 0.650 |
| i (°) | 19.3 | 18.4 | 19.4 |
| ω (°) | 22.2 | 22.2 | 22.1 |
| Ω (°) | 180.3 | 180.3 | 1802 |
| Π (°) | 202.5 | 202.5 | 202.4 |
| Tj | 2.95 | 2.93 | 2.93 |
| N | 103 | 132 | 76 |
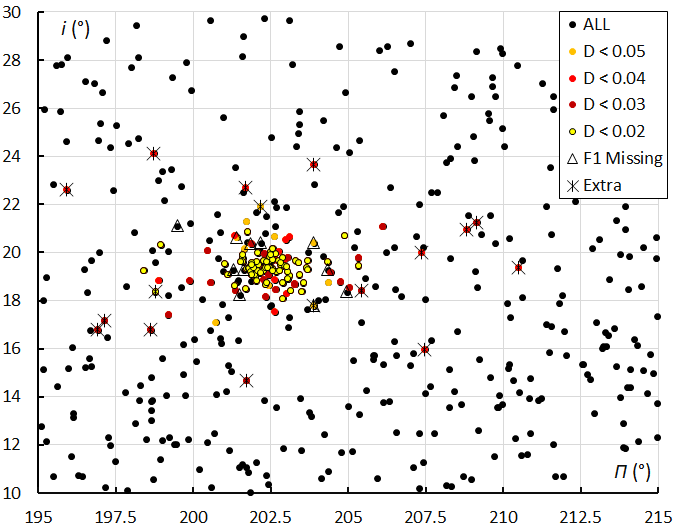
Figure 12 – The differences between both meteor shower search mentods plotted in the diagram of inclination i against the longitude of perihelion Π.
Figures 10 and 12 show the dense concentration around the longitude of perihelion at 202.5° and inclination between 18° and 20°. 11 orbits identified as M2025-F1 in the GMN orbit dataset failed to fulfill the DD < 0.05 criteria in the second search method. These orbits are marked with a triangle in Figure 12. The second method found 17 orbits that fulfilled the DD < 0.05 criteria but all these meteors are labelled as sporadics in the GMN orbit dataset. These orbits are crossed in Figure 12 and concern all outliers in inclination and longitude of perihelion although most of them fit the DD < 0.04 criterion. The discrepancy in the numbers comes from the difference in methods of selecting shower members. The initial method selects meteors within 2.5× the median distance from the median radiant, and within 5 sigma geocentric velocity (see Figure 3). The last method relies entirely on the orbit similarity criteria which may be too tolerant for some types of meteor showers. Both methods detect most of the orbits in common and the differences in both resulting orbit datasets according to the two different methods have no significant influence on the final mean orbits. Both methods confirm the detection of this new meteor shower and the final mean orbits are almost identical.
Comparing older data and other datasets
Looking up past years orbit data for Global Meteor Network (2018–2024, 1881758 orbits), we find 53 orbits with DD < 0.04. These orbits were detected in the time interval 346.0° < λʘ < 13.0°, 32 of these in 2024 but still too few to show any concentration on the radiant density plot for March 2024. The SonotaCo net orbit data (2007–2023, 490283 orbits) has only one orbit with DD < 0.04. EDMOND (2001–2023, 508266 orbits), has two orbits with DD < 0.04. The CAMS orbit data (2010–2016, 471582 orbits), has five orbits with DD < 0.04. We can conclude that this meteor shower produced too few orbits in earlier years to be detected.
Conclusion
A new meteor shower has been detected by the Global Meteor network. Its existence has been confirmed by two different meteor shower search methods. The orbit is a Jupiter-family comet type orbit. The parent body search did not return any candidates with a Southworth & Hawkins D criterion value of less than 0.1. This new meteor shower has been reported and registered as M2025-F1 in the Working List of Meteor Showers of the IAU-MDC.
Acknowledgment
This report is based on the data of the Global Meteor Network (Vida et al., 2020a; 2020b; 2021) which is released under the CC BY 4.0 license. We thank all 825 participants in the Global Meteor Network project for their contribution and perseverance. A list with the names of the volunteers who contribute to GMN has been published in the 2024 annual report (Roggemans et al., 2025).
References
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Jopek T. J., Rudawska R. and Pretka-Ziomek H. (2006). “Calculation of the mean orbit of a meteoroid stream”. Monthly Notices of the Royal Astronomical Society, 371, 1367–1372.
Roggemans P., Johannink C. and Campbell-Burns P. (2019a). “October Ursae Majorids (OCU#333)”. eMetN Meteor Journal, 4, 55–64.
Roggemans P., Campbell-Burns P., Kalina M., McIntyre M., Scott J. M. , Šegon D., Vida D. (2025). “Global Meteor Network report 2024”. eMetN Meteor Journal, 10, 67–101.
Šegon D., Vida D., Roggemans P. (2023). “New meteor shower in Draco”. eMetN Meteor Journal, 8, 171–176.
Southworth R. B. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithsonian Contributions to Astrophysics, 7, 261–285.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020a). “Estimating trajectories of meteors: an observational Monte Carlo approach – I. Theory”. Monthly Notices of the Royal Astronomical Society, 491, 2688–2705.
Vida D., Gural P., Brown P., Campbell-Brown M., Wiegert P. (2020b). “Estimating trajectories of meteors: an observational Monte Carlo approach – II. Results”. Monthly Notices of the Royal Astronomical Society, 491, 3996–4011.
Vida D., Šegon D., Gural P. S., Brown P. G., McIntyre M. J. M., Dijkema T. J., Pavletić L., Kukić P., Mazur M. J., Eschman P., Roggemans P., Merlak A., Zubrović D. (2021). “The Global Meteor Network – Methodology and first results”. Monthly Notices of the Royal Astronomical Society, 506, 5046–5074.